4.2. Систематические погрешности

В зависимости от характера измерений систематические погрешности подразделяются на постоянные, прогрессивные и систематические.

Постоянные систематические погрешности результатов измерений длительное время сохраняют свое значение. Такие погрешности имеют место в тех случаях, когда для измерения некоторой величины используется прибор, в градуировке которого имеется погрешность (например, погрешности мер длины, массы и т. п.).

Прогрессивные систематические погрешности – погрешности, которые в процессе измерений непрерывно возрастают или убывают во времени. К ним можно отнести погрешности, возникающие вследствие износа конструктивных деталей средств измерений, постепенного падения напряжения источника тока и т. п.

Периодические погрешности – это погрешности, значения которых являются периодической функцией времени или перемещения указателя измерительного прибора. Такие погрешности встречаются в индикаторах часового типа (в приборах с круговой шкалой).

В зависимости от причины появления систематические погрешности подразделяются:

• на субъективную погрешность измерения – составляющая погрешности измерения, обусловленная индивидуальными особенностями оператора;

• инструментальную погрешность измерения – составляющая погрешности измерения, обусловленная погрешностью применяемого средства измерений;

• погрешность метода измерений – составляющая погрешности измерения, обусловленная несовершенством принятого метода измерений;

• погрешность установки;

• погрешности влияющих величин (температуры, вибрации, относительной влажности воздуха и т. д.).

Систематические погрешности могут быть оценены до начала измерений и учтены путем:

 введения поправочного коэффициента (исключение погрешностей вычислением);

• оценки вероятности их границ и включением этого значения в общую погрешность результата измерений;

• исключение погрешностей в процессе измерения способами замещения, компенсации погрешностей;

• принятия мер для полного или частичного исключения источника возможных погрешностей до начала измерений.

4.3. Случайные погрешности

Случайные погрешности представляют собой погрешности, в появлении которых не наблюдается какой-либо закономерности. Случайные погрешности неизбежны и неустранимы и всегда присутствуют в результате измерений.

В основе теории случайных ошибок лежит предположение о том, что при большом числе измерений случайные погрешности одинаковой величины, но разного знака встречаются одинаково часто; большие погрешнос-ти встречаются реже, чем малые (вероятность появления погрешности уменьшается с ростом ее величины); при бесконечно большом числе измерений истинное значение измеряемой величины равно среднеарифметическому значению всех результатов измерений, а появление того или иного результата измерений как случайного события описывается нормальным законом распределения.

Чтобы понять, каким образом небольшие погрешности накладываются одна на другую в разных сочетаниях и как они влияют на результат параллельных определений, рассмотрим пример, когда суммарная случайная погрешность измерений формируется под действием четырех небольших, примерно равных по величине (₁ = ₂ = ₃ = ₄) элементарных погреш-ностей на разных этапах анализа. Условимся, что каждая из этих элементарных погрешностей проявляется в каждом параллельном определении с равной вероятностью либо отрицательно, либо положительно. В табл. 4.1 показаны все возможные сочетания этих погрешностей.

Таблица 4.1

Возможные сочетания четырех равных погрешностей на разных этапах анализа

Комбинации погрешностей	Величина суммарной случайной погрешности	Относительная частота появления этой погрешности
+1 + 2 +3 + 4	+4	1
–1 + 2 +3 + 4	+2	4
+1  2 +3 + 4	+2	4
+1 + 2  3 + 4	+2	4
+1 + 2 +3 – 4	+2	4
–1 – 2 + 3 + 4	0	6
–1 + 2 – 3 + 4	0	6
–1 + 2 + 3 – 4	0	6
+1 – 2 – 3 + 4	0	6
+1 – 2 + 3 – 4	0	6
+1 + 2 – 3 – 4	0	6
+1 – 2 – 3 – 4	2	4
–1 + 2 – 3 – 4	2	4
–1 – 2 + 3 – 4	2	4
–1 – 2 – 3 + 4	2	4
–1 – 2 – 3 – 4	4	1

Как видно из табл. 4.1, только одна комбинация может привести к максимальной положительной суммарной погрешности +4 и одна – к максимальной отрицательной погрешности –4. Четыре комбинации приводят к суммарной погрешности +2 и четыре – к максимальной отрицательной погрешности –2, шесть комбинаций  к нулевой суммарной погрешности. Соотношение 1 : 4 : 6 отражает вероятность появления случайных суммарных погрешностей, равных по абсолютной погрешности 4, 2 и 0.

Различают генеральную и выборочную совокупность измерений. Под генеральной совокупностью подразумевают все множество возможных значений х_i или возможных значений погрешностей Δх_i. Для выборочной совокупности число измерений n ограничено, и в каждом конкретном случае строго определяется. Обычно считается, что, если n  30, среднее значение данной совокупности измерений х_i достаточно приближается к его истинному значению.

Теория случайных ошибок позволяет оценить точность и надежность измерений при данном количестве замеров и определить минимальное количество замеров, гарантирующее требуемую точность и надежность измерений. Из теории вероятности известно, что наиболее универсальным способом описания случайных величин является описание их дифференциальных функций распределения, т. е. плотности распределения вероятности Р. Она всегда неотрицательная и подчиняется условию нормирования: 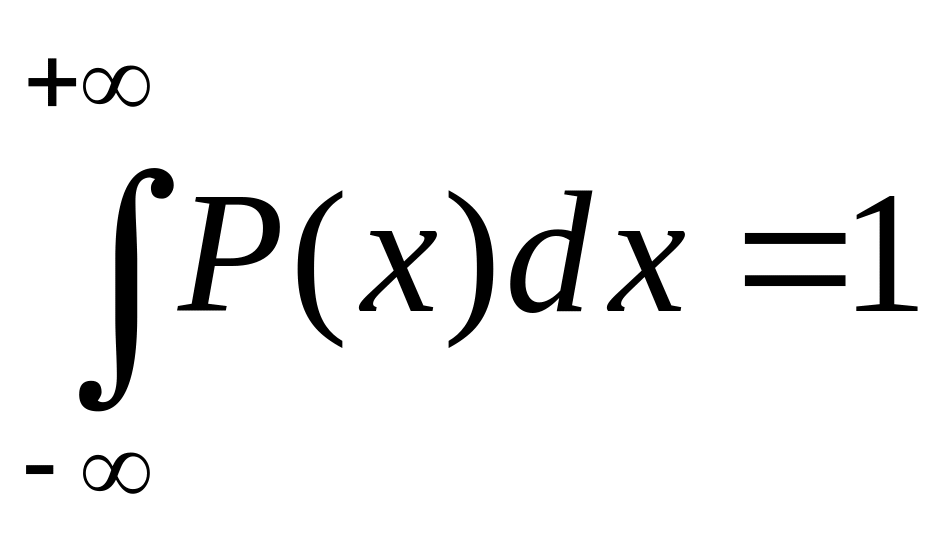. Достоверное событие имеет вероятность Р = 1, невоз-можное  Р = 0. Для случайного события , а сумма вероятностей всех возможных значений равна 1. Зависимость вероятности Р ожидания отдельных значений случайной величины от Этоэтих значений называется функцией распределения или рассеивания. Функция распределения может иметь любую форму.

Наиболее часто в качестве модели распределения случайных погрешностей применяется нормальный закон распределения (рис. 4.2).

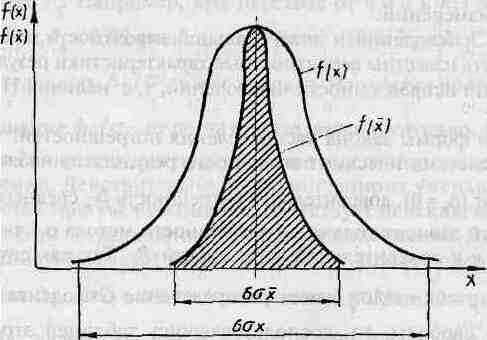
Рис. 4.2. Нормальный закон распределения случайных погрешностей

Мерой рассеивания результатов измерений является дисперсия D (или среднеквадратическое отклонение), которая вычисляется по формуле

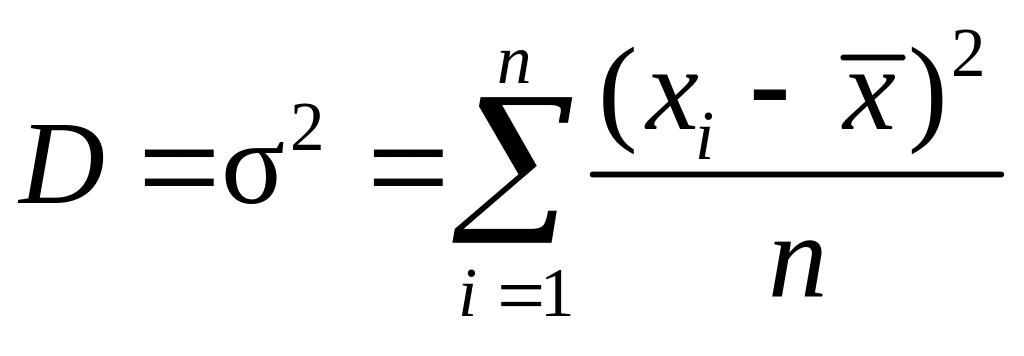. (4.6)

Значительно чаще в качестве меры рассеивания используется средне- квадратическое отклонение, которое определяют по формуле

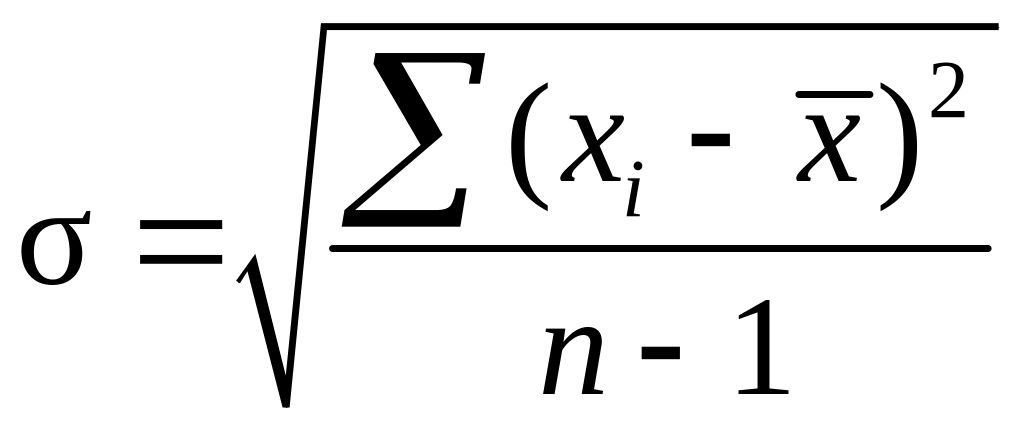. (4.7)

Чем меньше , тем меньше рассеивание (т. е. большинство наблюдений мало отличаются друг от друга), тем больше сходимость результатов измерений. Таким образом, несмотря на то что истинное значение измеряемой величины всегда остается неизвестным, с помощью математической статистики можно определить пределы области вокруг экспериментально найденного значения измеряемой величины, внутри которой следует ожидать с заданной степенью вероятности нахождение истинного значения. Пределы, найденные таким образом, называются доверительными границами, а интервал, ограниченный ими, – доверительным. Доверительный интервал характеризует точность измерений. Достоверность измерений (доверительная вероятность) (Р_д) – это вероятность того, что истинное значение измеряемой величины попадает в данный доверительный интервал. Эта величина определяется в долях или в процентах, для технологических расчетов она принимается равной 0,95, что означает: в заданный доверительный интервал из 100 измерений попадают 95. Значение (1  Р_д) называется уровнем значимости. Это значит, что при нормальном законе распределения погрешность, превышающая доверительный интервал, будет встречаться один раз из n измерений, где n = Р_д / (1  Р_д)

Если число измерений меньше 30, половина доверительного интервала

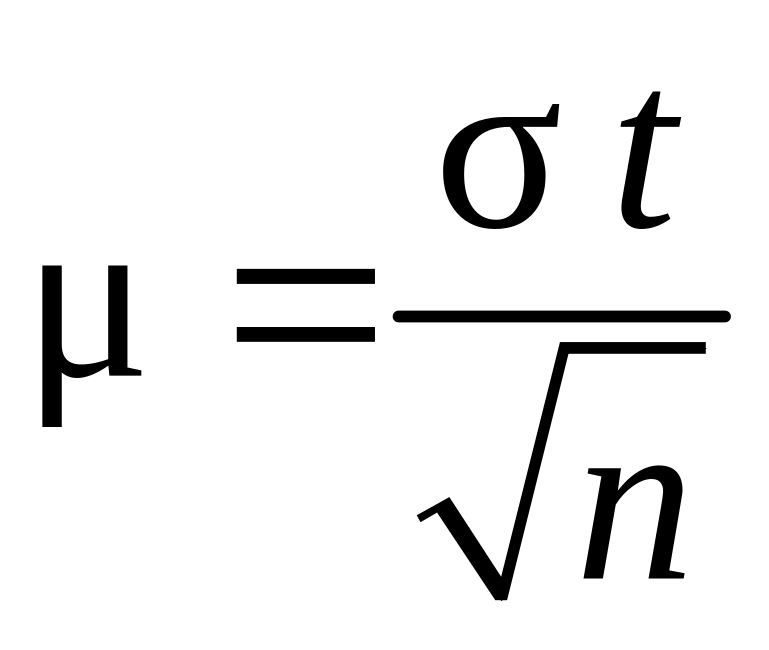, (4.8)

где, t- коэффициент Стьюдента, который определяют по табл.4.2.

действительное значение измеряемой величины

. (4.9)

Тогда доверительный интервал

. (4.10)

Доверительный интервал характеризует точность измерений, а доверительная вероятность – достоверность измерений. Ширина доверительного интервала  зависит:

 от величины рассеивания результатов измерений (от числа измерений);

 доверительной вероятности утверждения (доверительной вероят-ности).

Нет ссылки на табл. 4.2!!!

Таблица 4.2