Закон преломления

Доказательство закона преломления света исходя из принципа Ферма несколько более сложное, чем представленные выше.

Принцип Ферма представляет собой предельный случай принципа Гюйгенса-Френеля в волновой оптике для случая исчезающей малой длины волны света.

Дифракция - процесс искривления световых лучей, при прохождении их у края непрозрачных тел или сквозь небольшие отверстия, нарушающий законы геометрической оптики. Именно дифракция не позволяет различать сколь угодно малые детали предметов (накладывает ограничения на увеличение изображений в оптических приборах).

Проявляется дифракция света в том, что свет проникает в область геометрической тени в нарушение закона прямолинейного распространения света. Например, пропуская свет через маленькое круглое отверстие, обнаруживаем на экране светлое пятно большего размера, чем следовало ожидать при прямолинейном распространении.

Согласно принципу Гюйгенса-Френеля, волновое возмущение в точке P (рис.1), создаваемое источником P0, можно рассматривать как результат интерференции вторичных элементарных волн, излучаемых каждым элементом dS некоторой волновой поверхности S с радиусом r0. Амплитуда вторичных волн пропорциональна амплитуде первичной волны, приходящей в точку Q, площади элемента dS и убывает с возрастанием угла между нормалью к поверхности S и направлением излучения вторичной волны на точку P Амплитуда E_Q первичной волны в точке Q на поверхности S даётся выражением  , где A - амплитуда волны на расстоянии единицы длины от источника, k - волновой вектор,   - циклическая частота. Вклад в волновое возмущение в точке P, вносимый элементом поверхности dS, запишется в виде

,

(1)

где   - расстояние от точки Q до P,   - функция, описывающая зависимость амплитуды вторичных волн от угла  . Полное поле в точке наблюдения P представляется интегралом

.

(2)

Если за элемент поверхности взять площадь кольца, вырезаемого из волнового фронта S двумя бесконечно близкими концентрическими сферами с центрами в точке наблюдения P, и выразить dS через приращение  , то получим

.

(3)

Верхний предел интеграла R_max=R+2r₀. Функция теперь рассматривается как функция от  Точное вычисление (3) невозможно без знания  , однако Френель дал метод приближённого его вычисления, используя разбиение поверхности S на так называемые зоны Френеля. Вид функции   в принципе Гюйгенса-Френеля остается неопределенным, но при    ; множитель i означает, что фазы вторичных волн отличаются на   от фазы первичной волны в точке Q. Из математически точного определения принципа Гюйгенса-Френеля, данного Кирхгофом, следует и определение функции 

Зоны френеля

участки, на к-рые разбивают поверхность фронта световой волны для упрощения вычислений при определении амплитуды волны в заданной точке пр-ва. Метод З. Ф. используется при рассмотрении задач о дифракции волн в соответствии с Гюйгенса — Френеля принципом. Рассмотрим распространение монохроматической световой волны из точки Q(источник) в к.-л. точку наблюдения Р (рис.).

Согласно принципу Гюйгенса — Френеля, действие источника Q заменяют действием воображаемых источников, расположенных на вспомогат. поверхности S, в кач-ве к-рой выбирают поверхность фронта сферич. волны, идущей из Q. Далее поверхность S разбивают на кольцевые зоны так, чтобы расстояния от краёв зоны до точки наблюдения Р отличались на l/2: Ра=РО+l/2; Рb=Ра+l/2; Рс=Рb+l/2 (О — точка пересечения поверхности волны с линией PQ, l — длина волны). Образованные т. о. равновеликие участки поверхности S наз. З. Ф. Участок Оа сферич. поверхности S наз. первой З. Ф., аb — второй, bc — третьей З. Ф. и т. д. Радиус m-й З. Ф. в случае дифракции на круглых отверстиях и экранах определяется след. приближённым выражением (при ml<-r0):

где R — расстояние от источника до отверстия, r0 — расстояние от отверстия (или экрана) до точки наблюдения. В случае дифракции на прямолинейных структурах (прямолинейный край экрана, щель) размер m-й З. Ф. (расстояние внеш. края зоны от линии, соединяющей источник и точку наблюдения) приближённо равен O(mr0l).

Волн. процесс в точке Р можно рассматривать как результат интерференции волн, приходящих в точку наблюдения от каждой З. Ф. в отдельности, приняв во внимание, что амплитуда колебаний от каждой зоны медленно убывает с ростом номера зоны, а фазы колебаний, вызываемых в точке Р смежными зонами, противоположны. Поэтому волны, приходящие в точку наблюдения от двух смежных зон, ослабляют друг друга; амплитуда результирующего колебания в точке Р меньше, чем амплитуда, создаваемая действием одной центр. зоны.

Метод разбиения на З. Ф. наглядно объясняет прямолинейное распространение света с точки зрения волн. природы света. Он позволяет просто составить качественное, а в ряде случаев и достаточно точное количеств. представление о результатах дифракции волн при разл. сложных условиях их распространения. Экран, состоящий из системы концентрич. колец, соответствующих З. Ф. (см. ЗОННАЯ ПЛАСТИНКА), может дать, как и линза, усиление освещённости на оси или даже создать изображение. Метод З. Ф. применим не только в оптике, но и при изучении распространения радио- и звук. волн.

Математическая формулировка принципа Гюйгенса-Френеля

Пусть S - волновая поверхность, не закрытая препятствием, P - точка наблю-дения. Тогда элемент поверхности dS возбудит в точке P колебание: 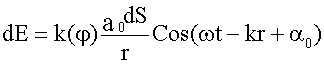Результирующее колебание: Здесь k( φ) определяет зависимость амплитуды dE от угла между нормалью к площадке dS и направлением на точку P. Множитель a0 дает амплитуду светового колебания в том месте, где находится dS. Величины ω и k - круговая частота и волновое число сферической волны (15.1.7.), распространяющейся от элемента dS.

Дифракция на круглом экране.

Рассмотрим опять точку на оси. Здесь начало вектора, определяющего амплитуду, находится в центральной точке N, конец – в конце последней закрытой зоны. Если закрыто мало зон, в точке на оси освещенность почти такая же, как и в отсутствии экрана. С увеличением числа зон освещенность падает. Но в середине все-таки светлое пятнышко. Вокруг – кольца.

Это явление явилось одним из первых доказательств волновой природы света (Араго). (Оно находило применение в фотографии – вместо объектива – шарик).

Но все это так получается только если отверстие, или экран – круглые с точностью до размеров зоны.

Светлое пятно в середине геометрической тени получило название пятно Пуассона.