27) Матричная запись слау и методы решения:

Матричная запись СЛАУ заключается в том, чтобы записать в матрицу коэффициенты при неизвестных переменных.

Методы решения:

Пусть задана СЛАУ

, Тогда в матричной форме

Метод обратной матрицы:

AX=B  AA^-1X=BA^-1  X=BA^-1

Метод Крамера:

Система линейных уравнений:

Если в системе det A≠0 и существует A^-1, то система имеет единственное решение.

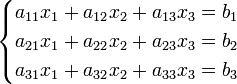
Определители:

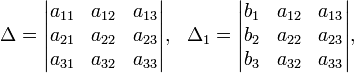
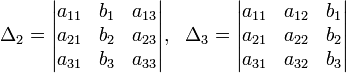
Заметим что ∆_i определитель получается из определителя ∆= с заменой i-го столбца на столбец свободных членов.

Решение:

Метод Гаусса:

1. Записать расширенную матрицу системы.

2. Привести к ступенчатому виду с помощью элементарных преобразований(Прямой ход Гаусса)

3. Провести обратный ход Гаусса (если нужно).

Пояснение: Возможны случаи когда решения очевидны после проведения прямого хода Гаусса. Но если же это не так, то из последнего ненулевого уравнения выражаем базисную переменную через небазисные и подставляем в предыдущие уравнения. Повторяя эту процедуру для всех базисных переменных, получаем фундаментальное решение.

Метод Жордана-Гаусса:

1. Выбирают первый слева столбец матрицы, в котором есть хоть одно отличное от нуля значение.

2. Если самое верхнее число в этом столбце есть ноль, то меняют всю первую строку матрицы с другой строкой матрицы, где в этой колонке нет нуля.

3. Все элементы первой строки делят на верхний элемент выбранного столбца.

4. Из оставшихся строк вычитают первую строку, умноженную на первый элемент соответствующей строки, с целью получить первым элементом каждой строки (кроме первой) ноль.

5. Далее проводят такую же процедуру с матрицей, получающейся из исходной матрицы после вычёркивания первой строки и первого столбца.

6. После повторения этой процедуры 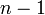  раз получают ступенчатую матрицу

7. Вычитают из предпоследней строки последнюю строку, умноженную на соответствующий коэффициент, с тем, чтобы в предпоследней строке осталась только 1 на главной диагонали.

8. Повторяют предыдущий шаг для последующих строк. В итоге получают единичную матрицу и решение на месте свободного вектора (с ним необходимо проводить все те же преобразования).

9. Чтобы получить обратную матрицу, нужно применить все операции в том же порядке к единичной матрице.

29) Ранг Матрицы. Теорема Кронекера – Капелле.

Рангом системы строк (столбцов) матрицы   с   строк и   столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.

Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.

Теорема Кронекера – Капелле:

Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.

Док-во:

1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход А->А* не изменяют ранга.

2) Если RgA = RgA*, то это означает, что они имеют один и тот же базисный минор (минор ранга n базисный, если все миноры n+1 ранга равны 0 либо не существуют)

Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше.

33) Изменение матрицы линейного преобразования при замене базиса.

Преобразование матрицы линейного оператора при изменении базиса.

Как уже отмечалось, в пространстве Rⁿ существует множество различных базисов.

Пусть и — два базиса в Rⁿ.

Обозначим и координаты векторов X и Y из L и матрицу оператора A соответственно в базисах и , а – матрицу перехода от базиса к базису , т.е.

Тогда

откуда имеем формулы преобразования матрицы линейного оператора при изменении базиса: