23. Формула Муавра. Извлечения корня из комплексного числа.

Формула Муавра позволяет возводить комплексное число в n-ую степень.

Формула Муавра для показательной формы:

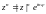
Формула Муавра для тригонометрической формы:

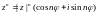
Док-во формулы Муавра.

По индукции: (cos x + i sin x)^1 = cos 1x + i sin 1x (cos x + i sin x)^(n+1)=(cos x + i sin x)^n*(cos x + i sin x)=(cos nx + i sin nx)(cos x + i sin x) = = (cos nx cos x - sin nx sin x) + i (cos nx sin x + sin nx cos x) = cos (n+1)x + sin (n+1)x.

Пусть a = |a|e^iϕ – Фиксированное комплексное число, тогда:

Уравнение zⁿ=a имеет ровно n различных решений (z₀, z₁, ... , z_n-1), причем решения даются формулой:

, где k=0, 1, … , n-1.

Число 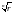- действительное положительное, Числа z_k (k=0, 1, … , n-1) называются корнями n-й степени из комплексного числа a (обозн. ).

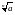24) Матрица. Размер матрицы. Квадратная матрица и её порядок. Равенство матриц. Вектор-строка и вектор-столбец. Линейные операции над матрицами.

Матрица размера (m на n) – прямоугольная таблица из m на n чисел a_{i, j}, где i=(1, 2, … , m) j=(1, 2, … , n).

Если число строк и столбцов матрицы равны, то такую матрицу называют квадратной, а число строк и столбцов называют порядком квадратной матрицы.

Две матрицы считаются равными, если они имеют одинаковую размерность и их соответствующие элементы равны.

Векторы бывают двух видов — векторы-строки и векторы-столбцы. Векторы-строки записываются в виде упорядоченной строки, векторы-столбцы записываются в виде упорядоченного столбца (нумерация компонент вектора-столбца идет сверху).

Пусть   и   — матрицы одинаковых размеров  . Матрица   тех же размеров   называется суммой матриц   и  , если ее элементы равны сумме соответствующих элементов матриц   и  :      . Сумма матриц обозначается  .

Произведением матрицы   и числа   называется матрица   тех же размеров, что и матрица  , каждый элемент которой равен произведению числа   на соответствующий элемент матрицы 

25) Умножение матриц, его ассоциативность, дистрибутивность относительно сложения и некомутативность. Единичная матрица. Её строение и единственность (для квадратных матриц данного порядка).

Произведением AB (m на n) матрицы А = (a_{i j)} на (n на k) матрицу B = (b_{i j}) называется

(m на k) матрица С = (c_{i j}), элемент которой d_{i j}, стоящий в i-й строке и j-м столбце, равен сумме произведений соответствующих элементов i-й строки матрицы А и j-го столбца матрицы В.

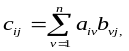i=1, 2, …, m. j=1, 2, …, k

A(BC)=(AB)C

A(B+C)=AB+AC

AB≠BA

Единичная матрица — квадратная матрица, элементы главной диагонали которой равны единице, а остальные равны нулю.

Единичная матрица – такая матрица, что умножение на неё матрицы того же порядка образуется исходная матрица.

Единичная матрица для матриц своего порядка единственна.

26) Обратная матрица и её построение.

Обратная матрица — такая матрица A^-1, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:

Квадратная матрица имеет обратную  когда она невырожденная, то есть её определитель не равен нулю.

Методы нахождения обратной матрицы:

Метод Гаусса-Жордана:

Приписать к исходной матрице А единичную Е. Применяя элементарные преобразования к исходной матрице А, приводим её к единичной, параллельно делая эти же операции к приписанной матрице. В итоге, когда мы приведём исходную матрицу к единичной, приписанная матрица станет обратной.

Метод алгебраических дополнений:

1. Находим определитель матрицы А.

2. Находим все алгебраические дополнения исходной матрицы А.

3. Составляем матрицу из алгебраических дополнений каждого элемента матрицы А и транспонируем её.

4. Умножаем полученную транспонированную матрицу на

5. Получаем обратную матрицу А^-1