Векторное произведение в координатной форме. Площадь параллелограмма, построенного на двух векторах в пространстве.
Если два вектора a и b определены своими декартовыми прямоугольными координатами
a = {X1, Y1, Z1}, b = {X2, Y2, Z2},
то векторное произведение этих векторов имеет вид
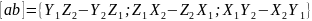
или
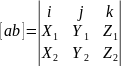
Если два вектора a = {X1, Y1, Z1}, b = {X2, Y2, Z2}, коллинеарны, то координаты их пропорциональны, т. е.
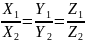
Длина (или модуль) векторного произведения [ab] равняется площади S параллелограмма, построенного на приведенных к общему началу векторах a и b.
Смешанное произведение векторов. Его выражение через координаты сомножителей. Свойства смешанного произведения. Условие компланарности трех векторов. Геометрический смысл смешанного произведения.
Пусть даны три произвольных вектора a, b и c. Если вектор a векторно умножается на вектор b, а затем получившийся при этом вектор [ab] скалярно умножается на вектор c, то в результате получается число [ab]c, называемое смешанным произведением векторов a, b и c.
Если векторы a, b, c заданы своими координатами: a = {X1, Y1, Z1}, b = {X2, Y2, Z2}, с = {X3, Y3, Z3}, то смешанное произведение [ab]c определяется формулой:
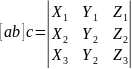
Три вектора компланарны их смешанное произведение = 0.
Смешанное произведение [ab]c равно объему параллелепипеда, построенного на приведенных к общему
началу векторах a, b и c, взятому со знаком плюс, если тройка abc правая, и со знаком минус, если тройка abc левая. Если же векторы a, b и c компланарны, то [ab]c равно нулю.
Свойства:
Справедливо равенство [ab]c = a[bc].
Смешанное произведение трех векторов, два из которых совпадают, равно нулю.
Уравнение прямой на плоскости и плоскости в пространстве, проходящей через данную точку перпендикулярно данному вектору. Геометрический смысл коэффициентов при неизвестных.
17. Уравнение прямой в пространстве. В каноническом и параметрическом виде. Уравнение прямой, проходящей через 2 данные точки.
Каждый ненулевой вектор, лежащий на прямой или на параллельной прямой называется направляющим вектором данной прямой.
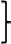Пусть
известна точка M(x0,y0,z0)
и направляющий вектор а(l;
m;
n).
Тогда уравнение прямой в пространстве
можно задать двумя уравнениями
;
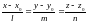(канонический
вид).
Пусть
,
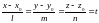тогда
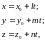Также уравнение прямой. (параметрический
вид).
Если нам даны 2 точки (пусть M1(x1, y1,z1) и M2 (x2, y2,z2)) то можно найти вектор q={x2- x1; y2- y1; z2-z1}
Который будет направляющим для прямой, проходящей через 2 данные точки. Тогда получаем:
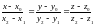каноническое
уравнение прямой проходящей через 2
данные точки.
18. Переход к каноническому виду уравнения прямой в пространстве от задания её в виде пересечения двух плоскостей.
Уравнение прямой P в пространстве может быть задано с помощью двух уравнений пересекающихся плоскостей L1 и L2. M=L1∩L2
L1
=
A1(x-x0)+B1(y-y0)+C1(z-z0)=0;
L2= A2(x-x0)+B2(y-y0)+C2(z-z0)=0 Уравнение прямой в пространстве (общее) (При условии, что нормаль-векторы этих плоскостей не коллинеарны.
Можно перейти к каноническому виду этого уравнения следующим путём:
Найти хотя бы одно решение данной системы уравнений. Пусть это будет точка a(x1, y1, z1).
Найти векторное произведение нормаль-векторов этих плоскостей q[n1; n2], где
n1={A1, B1, C1} и n2{A2, B2, C2}. Вектор q будет направляющим для искомой прямой.
q
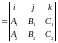= λ1i+λ2+λ3k
Тогда каноническое уравнение будет иметь вид
;