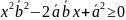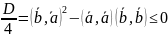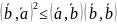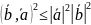- •Определители второго и третьего порядка и их вычисление. Определение определителя любого порядка. Алгебраические дополнения. Перечислить свойства определителя.
- •Определение вектора. Равенство векторов. Сумма векторов и ее свойства. Произведения векторов и числа и его свойства.
- •Проекция на ось суммы векторов, произведения вектора и числа и их свойства.
- •Разложение вектора по базису. Координатное представление.
- •Координаты вектора и точки в декартовой системе координат.
- •Длина вектора. Расстояние между двумя точками. Орт вектора. Координаты орта. Косинусы направления.
- •Линейные операции над векторами в координатной форме. Условие коллинеарности двух векторов. Деление отрезка в данном отношении и, в частности, пополам.
- •Скалярное произведение двух векторов. Его определение через взаимные прямоугольные проекции. Неравенство Коши.
- •Свойства скалярного произведения векторов. Скалярное произведение в координатной форме в декартовом базисе.
- •Модуль вектора. Косинус угла между векторами. Условие перпендикулярности двух векторов.
- •Площадь параллелограмма, построенного из двух векторов в плоскости.
- •Ориентация системы координат. Правая и левая тройки векторов. Определение векторного произведения. Свойства векторного произведения.
- •Векторное произведение в координатной форме. Площадь параллелограмма, построенного на двух векторах в пространстве.
- •Уравнение прямой на плоскости и плоскости в пространстве, проходящей через данную точку перпендикулярно данному вектору. Геометрический смысл коэффициентов при неизвестных.
- •17. Уравнение прямой в пространстве. В каноническом и параметрическом виде. Уравнение прямой, проходящей через 2 данные точки.
- •18. Переход к каноническому виду уравнения прямой в пространстве от задания её в виде пересечения двух плоскостей.
- •19. Уравнение плоскости, проходящей через данную точку, параллельную двум данным векторам. Уравнение плоскости, проходящей через 3 данные точки.
- •20. Комплексные числа и арифметические операции над ними
- •21. Сопряженные комплексные числа. Корни многочлена с вещественными коэффициентами.
- •22. Тригонометрическая и показательная форма к.Ч. Умножение и деление к.Ч. В тригон. И показат. Форме
- •23. Формула Муавра. Извлечения корня из комплексного числа.
- •24) Матрица. Размер матрицы. Квадратная матрица и её порядок. Равенство матриц. Вектор-строка и вектор-столбец. Линейные операции над матрицами.
- •25) Умножение матриц, его ассоциативность, дистрибутивность относительно сложения и некомутативность. Единичная матрица. Её строение и единственность (для квадратных матриц данного порядка).
- •26) Обратная матрица и её построение.
- •27) Матричная запись слау и методы решения:
- •29) Ранг Матрицы. Теорема Кронекера – Капелле.
- •35) Приведение квадратичной формы к каноническому виду.
- •36)Закон Инерции Квадратичных форм
- •37) Симметричный оператор. Инвариантность ортогонального дополнения собственного вектора.
- •41)Приведение квадратичной формы к каноническому виду изометрическим линейным преорбазованием.
- •42)Напомнить индуктивное определение определителя. Разложение по первой строке. Перестановка двух строк.
- •43)Разложение определителя по любой строке.
- •44)Транспонирование определителя.
- •45)Определитель произведения двух квадратных матриц.
- •46)Группы. "Экономное" опеределение. Единственность и перестановочность левой единицы и левого обратного.
- •47)Подгруппы. Разложение по подгруппе. Теорема Лагранжа.
- •48)Нормальные подгруппы. Фактор-группы. Циклические группы. Гомоморфизмы групп.
Длина вектора. Расстояние между двумя точками. Орт вектора. Координаты орта. Косинусы направления.
Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора. Для обозначения модуля вектора используются две вертикальные линии слева и справа | |.
Величина М1М2 направленного отрезка М1М2 равна x2 — х1 т. е. М1М2 = х2-х1.
Рассмотрим
в пространстве декартову систему
координат Oxyz
и точки M1(x1,y1,z1)
и М2{х2, у2, z2)
Расстояние ρ(М1,
М2)
между точками М1
и М2,
равное длине направленного отрезка
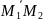 ,
равно также длине диагонали параллелепипеда,
грани которого параллельны координатным
плоскостям и проходят через точки М1
и М2.
Длина параллельного оси Ох ребра этого
параллелепипеда равна, абсолютной
величине проекции отрезка М1М2
на ось Ох, т. е., согласно формуле равна
|x1
—x2|.
По аналогичным соображениям длины
ребер, параллельных осям Оу и Oz,
равны соответственно |y2
— y1|
и |z2
— z1|.
,
равно также длине диагонали параллелепипеда,
грани которого параллельны координатным
плоскостям и проходят через точки М1
и М2.
Длина параллельного оси Ох ребра этого
параллелепипеда равна, абсолютной
величине проекции отрезка М1М2
на ось Ох, т. е., согласно формуле равна
|x1
—x2|.
По аналогичным соображениям длины
ребер, параллельных осям Оу и Oz,
равны соответственно |y2
— y1|
и |z2
— z1|.
Используя теорему Пифагора, получим следующую формулу для ρ(М1, М2):
ρ(М1,
М2)
=
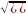
Формула расстояния между двумя точками в случае их расположения в плоскости Оху имеет следующий вид:
ρ(М1, М2) =
Ортом произвольного ненулевого вектора c назовем единичный вектор, коллинеарный c и имеющий одинаковое с c направление.
Координаты
орта - координаты a0(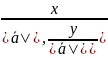 ),
где a0 орт
вектор.
),
где a0 орт
вектор.
Косинусы направления вектора - это косинусы углов, которые образует вектор с осями координат.
Линейные операции над векторами в координатной форме. Условие коллинеарности двух векторов. Деление отрезка в данном отношении и, в частности, пополам.
Линейные операции над векторами в координатной форме:
a={X1,Y1,Z1}, b={X2,Y2,Z2}.
Сложение. a + b={X1 + X2; Y1 + Y2; Z1+ Z2};
Разность. a - b={X1 - X2; Y1 - Y2; Z1- Z2};
Умножение. α*a={α*X1; α*Y1; α*Z1};
Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными. Признаком коллинеарности двух векторов a={X1,Y1,Z1} и b={X2,Y2,Z2} является пропорциональность координат:
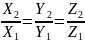
Рассмотрим
в пространстве две различные точки
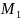 и
и
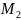 и прямую, определяемую этими точками.
Выберем на этой прямой некоторое
направление. На полученной оси точки
M1
и M2
определяют направленный отрезок
.
Пусть М — любая отличная от
точка указанной выше оси. Число
λ=
и прямую, определяемую этими точками.
Выберем на этой прямой некоторое
направление. На полученной оси точки
M1
и M2
определяют направленный отрезок
.
Пусть М — любая отличная от
точка указанной выше оси. Число
λ=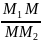 называется
отношением, в котором точка M
делит направленный отрезок
.
Таким образом, любая, отличная от M2
называется
отношением, в котором точка M
делит направленный отрезок
.
Таким образом, любая, отличная от M2
точка M делит отрезок в некотором отношении λ, где λ определяется равенством λ= .
Согласно
М1М2
= х2-х1,
получаем М1M
= x
— x1,
a
MМ2
= x2—
х,
следовательно λ=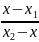 =>
x=
=>
x=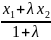
Совершенно аналогично вычисляются координаты y и z точки M.
Таким
образом: x=
,
y=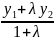 ,
z=
,
z=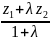 .
.
Эти формулы называются формулами деления отрезка в данном отношении λ.
Очевидно,
если λ=1, то точка М делит отрезок
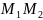 пополам. Получающиеся формулы (из
соотношений x=
,
y=
,
z=
)
называются формулами деления отрезка
пополам.
пополам. Получающиеся формулы (из
соотношений x=
,
y=
,
z=
)
называются формулами деления отрезка
пополам.
x=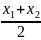 ,
y=
,
y=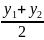 ,
z=
,
z=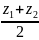 .
.
Скалярное произведение двух векторов. Его определение через взаимные прямоугольные проекции. Неравенство Коши.
Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
Скалярное произведение векторов a и b будем обозначать символом ab. Если угол между векторами a и b равен ϕ, то по определению скалярное произведение этих двух векторов выражается формулой
ab = |a||b|cosϕ.
Т.к. проекция вектора b на ось u равна длине вектора b, умноженной на косинус ϕ угла наклона вектора b
к оси u, то ab = |a||b|cosϕ = |a|прba
Скалярным произведением двух векторов называется число, равное произведению длины одного
из этих векторов на проекцию другого вектора на ось, определяемую первым из указанных векторов.
Неравенство Коши.

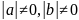
Рассмотрим вектор (xb-a)2