
- •Определители второго и третьего порядка и их вычисление. Определение определителя любого порядка. Алгебраические дополнения. Перечислить свойства определителя.
- •Определение вектора. Равенство векторов. Сумма векторов и ее свойства. Произведения векторов и числа и его свойства.
- •Проекция на ось суммы векторов, произведения вектора и числа и их свойства.
- •Разложение вектора по базису. Координатное представление.
- •Координаты вектора и точки в декартовой системе координат.
- •Длина вектора. Расстояние между двумя точками. Орт вектора. Координаты орта. Косинусы направления.
- •Линейные операции над векторами в координатной форме. Условие коллинеарности двух векторов. Деление отрезка в данном отношении и, в частности, пополам.
- •Скалярное произведение двух векторов. Его определение через взаимные прямоугольные проекции. Неравенство Коши.
- •Свойства скалярного произведения векторов. Скалярное произведение в координатной форме в декартовом базисе.
- •Модуль вектора. Косинус угла между векторами. Условие перпендикулярности двух векторов.
- •Площадь параллелограмма, построенного из двух векторов в плоскости.
- •Ориентация системы координат. Правая и левая тройки векторов. Определение векторного произведения. Свойства векторного произведения.
- •Векторное произведение в координатной форме. Площадь параллелограмма, построенного на двух векторах в пространстве.
- •Уравнение прямой на плоскости и плоскости в пространстве, проходящей через данную точку перпендикулярно данному вектору. Геометрический смысл коэффициентов при неизвестных.
- •17. Уравнение прямой в пространстве. В каноническом и параметрическом виде. Уравнение прямой, проходящей через 2 данные точки.
- •18. Переход к каноническому виду уравнения прямой в пространстве от задания её в виде пересечения двух плоскостей.
- •19. Уравнение плоскости, проходящей через данную точку, параллельную двум данным векторам. Уравнение плоскости, проходящей через 3 данные точки.
- •20. Комплексные числа и арифметические операции над ними
- •21. Сопряженные комплексные числа. Корни многочлена с вещественными коэффициентами.
- •22. Тригонометрическая и показательная форма к.Ч. Умножение и деление к.Ч. В тригон. И показат. Форме
- •23. Формула Муавра. Извлечения корня из комплексного числа.
- •24) Матрица. Размер матрицы. Квадратная матрица и её порядок. Равенство матриц. Вектор-строка и вектор-столбец. Линейные операции над матрицами.
- •25) Умножение матриц, его ассоциативность, дистрибутивность относительно сложения и некомутативность. Единичная матрица. Её строение и единственность (для квадратных матриц данного порядка).
- •26) Обратная матрица и её построение.
- •27) Матричная запись слау и методы решения:
- •29) Ранг Матрицы. Теорема Кронекера – Капелле.
- •35) Приведение квадратичной формы к каноническому виду.
- •36)Закон Инерции Квадратичных форм
- •37) Симметричный оператор. Инвариантность ортогонального дополнения собственного вектора.
- •41)Приведение квадратичной формы к каноническому виду изометрическим линейным преорбазованием.
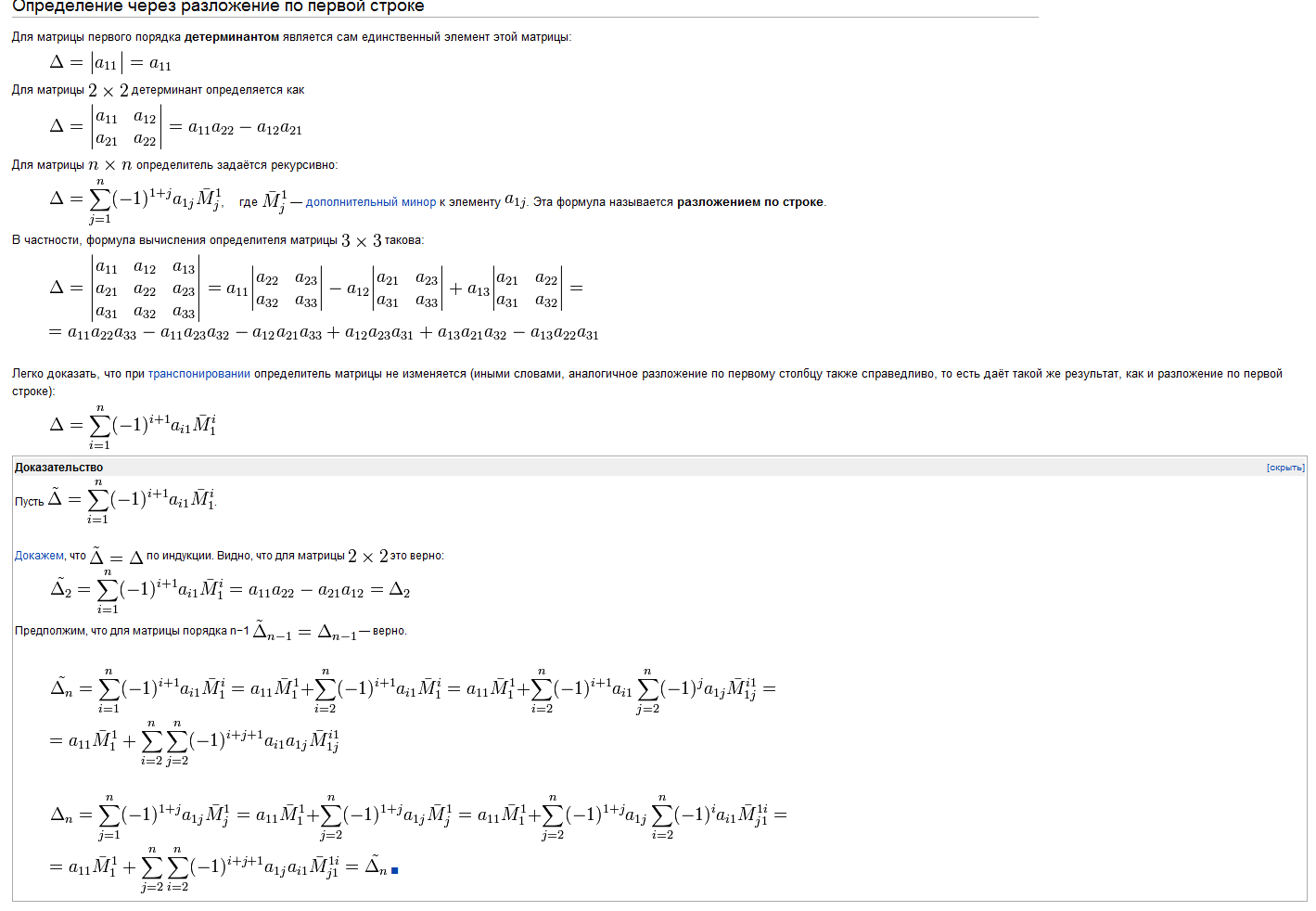
- •42)Напомнить индуктивное определение определителя. Разложение по первой строке. Перестановка двух строк.
- •43)Разложение определителя по любой строке.
- •44)Транспонирование определителя.
- •45)Определитель произведения двух квадратных матриц.
- •46)Группы. "Экономное" опеределение. Единственность и перестановочность левой единицы и левого обратного.
- •47)Подгруппы. Разложение по подгруппе. Теорема Лагранжа.
- •48)Нормальные подгруппы. Фактор-группы. Циклические группы. Гомоморфизмы групп.
41)Приведение квадратичной формы к каноническому виду изометрическим линейным преорбазованием.
Приведение квадратичных форм к каноническому виду
Рассмотрим некоторое линейное преобразование А с матрицей .
Это симметрическое преобразование можно записать в виде:
y1 = a11x1 + a12x2
y2 = a12x1 + a22x2
где у1 и у2 – координаты вектора в базисе .
Очевидно, что квадратичная форма может быть записана в виде
Ф(х1, х2) = х1у1 + х2у2.
Как видно, геометрический смысл числового значения квадратичной формы Ф в точке с координатами х1 и х2 – скалярное произведение .
42)Напомнить индуктивное определение определителя. Разложение по первой строке. Перестановка двух строк.
43)Разложение определителя по любой строке.
Рассмотрим квадратную матрицу A n-го порядка.
Выберем i,j-ый элемент этой матрицы и вычеркнем i-ую строку и j-ый столбец. В результате мы получаем матрицу (n – 1)-го порядка, определитель которой называется минором элемента и обозначается символом Mi j:
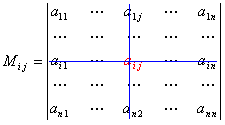
Алгебраическое
дополнение Ai,j элемента ai j
определяется формулой
![]()
Теорема о разложении определителя по элементам строки. Определитель матрицы A равен сумме произведений элементов строки на их алгебраические дополнения:
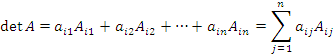
Теорема о разложении определителя по элементам столбца. Определитель матрицы A равен сумме произведений элементов столбца на их алгебраические дополнения:
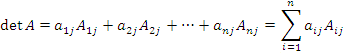
Теоремы о разложении определителя имеют важное значение в теоретических исследованиях. Они устанавливают, что проблема вычисления определителя n-го порядка сводится к проблеме вычисления n определителей (n –1)-го порядка.
Доказательство. По определению, детерминант матрицы A представляет собой сумму
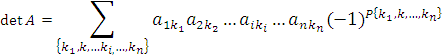
по всем возможным перестановкам индексов, нумерующих столбцы.
Выберем произвольным образом некоторую строку, например, с номером i.
Один
из элементов этой строки представлен
в каждом произведении
![]() . Поэтому слагаемые суммы (*) можно
перегруппировать, объединив в первую
группу те, что содержат элемент a11
в качестве общего множителя, во вторую
группу – члены, содержащие элемент a12
и т.д.
. Поэтому слагаемые суммы (*) можно
перегруппировать, объединив в первую
группу те, что содержат элемент a11
в качестве общего множителя, во вторую
группу – члены, содержащие элемент a12
и т.д.
Другими словами, выражение (*) можно представить в виде линейной комбинации элементов ai j (j = 1,2,…,n):
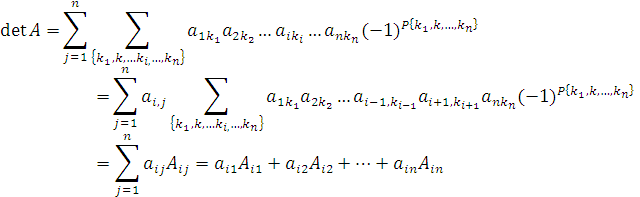 где
где
![]()
представляет собой минор элемента ai j .
Таким образом, и, следовательно, представляет собой алгебраическое дополнение элемента ai j.
Поскольку
![]() , то тем самым доказана и Теорема о
разложении определителя по элементам
столбца.
, то тем самым доказана и Теорема о
разложении определителя по элементам
столбца.
44)Транспонирование определителя.
При
транспонировании определитель матрицы
не изменяется (иными словами, аналогичное
разложение по первому столбцу также
справедливо, то есть даёт такой же
результат, как и разложение по первой
строке):
![]()

45)Определитель произведения двух квадратных матриц.
Определитель
произведения двух квадратных матриц
равен произведению определителей этих
квадратных матриц, т.е.
![]()
46)Группы. "Экономное" опеределение. Единственность и перестановочность левой единицы и левого обратного.
Понятие группы
Определение 1. Множество А, в котором определен закон композиции Т, называется группой G, если этот закон ассоциативен, существует нейтральный элемент е относительно закона Т и для каждого элемента а множества А существует обратный элемент а-1, т. е. такой элемент, для которого аТа-1 = е.
Если использовать мультипликативную форму записи композиции элементов, то определению 1 можно придать следующую форму.
Определение 2. Множество А элементов а, Ь, с ..., котором определен закон композиции, называемый умножением и ставящий в соответствие каждой паре элементов а, Ь множества А определенный элемент с = ab этого множества, называется группой G, если этот закон удовлетворяет следующим требованиям:
1°. a (bс) — (ab)c {ассоциативность).
2°. Существует элемент е множества А такой, что для любого элемента а этого множества ае = а (существование нейтрального элемента).
3°. Для любого элемента а множества А существует обратный элемент а-1такой, что аа-1 = е.
Обычно нейтральный элемент е называется единицей группы G. Если закон композиции Т, действующий в группе G, является коммутативным, то группа G называется коммутативной или абелевой. Для абелевых групп часто используется аддитивная форма записи композиции элементов. В этом случае нейтральный элемент абелевой группы называется нулем.
