Контрольные работы для студентов 1 курса направлений подготовки бакалавров 080100 - Экономика (профили: Экономика организации, Бухгалтерский учет и аудит) и 080200 Менеджмент

Индивидуальный номер варианта соответствует последней цифре номера зачетной книжки. Последняя цифра «0» соответствует десятому варианту.

Контрольная работа по предмету «Математический анализ»

Вариант - 1

1. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления:

а) б) в) г)

2. Исследовать функцию на непрерывность: найти точки разрыва функции и определить их тип. Построить схематический график функции.

3. Найти производные следующих функций:

а) ; б) ; в)

4. Составить уравнение касательной и нормали к графику кривой y = f(x) в точке, абсцисса которой равна .

5. Пользуясь правилом Лопиталя найти пределы функций:

а) ; б) .

6. Построить график функции y=f(x), используя общую схему исследования функций.

7. Найти неопределенные интегралы

   а) ;

   б) ;

   в) .

8. Воспользовавшись соответствующим приложением предельного интеграла к задачам геометрии, найти следующее:

а) площадь фигуры, ограниченную линиями:

б) Объем тела, образованного вращением вокруг оси фигуры, ограниченной линиями.

,

9. Найти общее решение дифференциального уравнения и его частное решение, удовлетворяющее начальным условиям при х = х₀ .

10. Найти область сходимости степенного ряда .

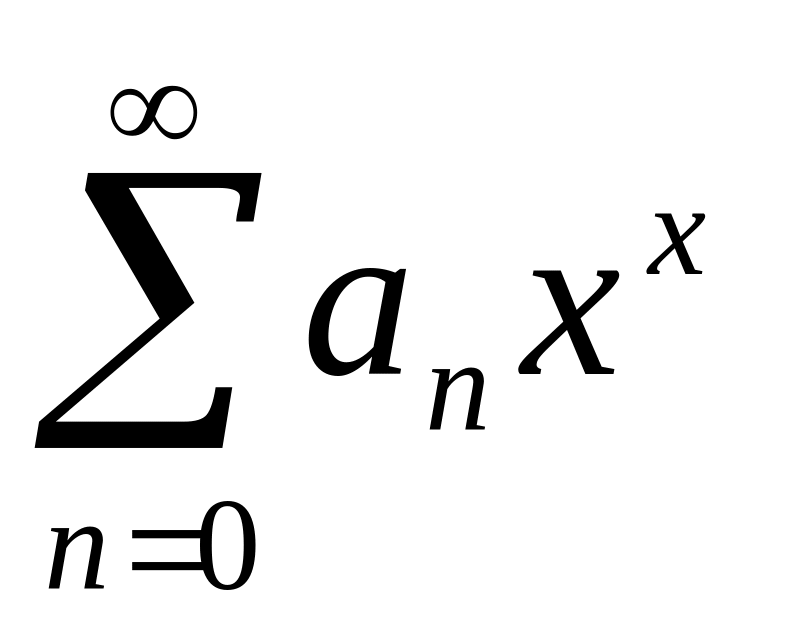Контрольная работа по предмету «Математический анализ»

Вариант – 2

1. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления:

2. Исследовать функцию на непрерывность: найти точки разрыва функции и определить их тип. Построить схематический график функции.

3. Найти производные следующих функций:

а) ; б) ; в) .

4. Составить уравнение касательной и нормали к графику кривой y = f(x) в точке, абсцисса которой равна .

5. Пользуясь правилом Лопиталя найти пределы функций:

а) ; б)

6. Построить график функции y=f(x), используя общую схему исследования функций.

7. Найти неопределенные интегралы

   а) ;

   б) ;

   в) .

8. Воспользовавшись соответствующим приложением предельного интеграла к задачам геометрии, найти следующее:

а) площадь фигуры, ограниченную линиями:

б) Объем тела, образованного вращением вокруг оси фигуры, ограниченной линиями.

, , ,

9. Найти общее решение дифференциального уравнения и его частное решение, удовлетворяющее начальным условиям при х = х₀ .

10. Найти область сходимости степенного ряда .

Контрольная работа по предмету «Математический анализ»

Вариант – 3

1. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления:

2. Исследовать функцию на непрерывность: найти точки разрыва функции и определить их тип. Построить схематический график функции.

3. Найти производные следующих функций:

а) ; б) ; в) .

4. Составить уравнение касательной и нормали к графику кривой y = f(x) в точке, абсцисса которой равна .

5. Пользуясь правилом Лопиталя найти пределы функций:

а) ; б) .

6. Построить график функции y=f(x), используя общую схему исследования функций.

7. Найти неопределенные интегралы

   а) ;

   б) ;

   в) .

8. Воспользовавшись соответствующим приложением предельного интеграла к задачам геометрии, найти следующее:

а) площадь фигуры, ограниченную линиями:

б) Объем тела, образованного вращением вокруг оси фигуры, ограниченной линиями.

, ,

9. Найти общее решение дифференциального уравнения и его частное решение, удовлетворяющее начальным условиям при х = х₀ .

10. Найти область сходимости степенного ряда .

Контрольная работа по предмету «Математический анализ»