2. Определение сезонных колебаний.
Для определения во временном ряду сезонных колебаний воспользуемся критерием, основанным на сравнении распределения коэффициентов автокорреляции. Последовательность коэффициентов автокорреляции называется автокорреляционной функцией. График это функции называется коррелограммой.
Анализ коррелограммы и автокорреляционной функции позволяет определить лаг. Построим автокоррелограмму и определим лаг.
Лаг |
Коэффициент автокорреляции |
1 |
0,722925 |
2 |
0,655045 |
3 |
0,651933 |
4 |
0,945934 |
5 |
0,592986 |
6 |
0,539753 |
7 |
0,552501 |
8 |
0,916298 |
9 |
0,361464 |
10 |
0,308634 |
11 |
0,44076 |
12 |
0,917905 |
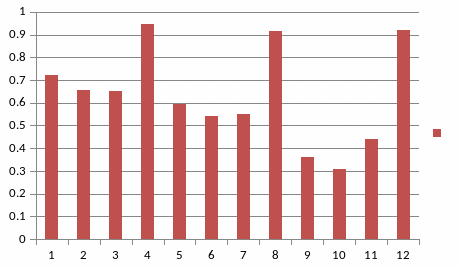
Рис. 3. Построено по коэффициенту корреляции.
Лаг равен 4.
Аддитивная модель.
1) Сгладим временной ряд центрированной скользящей средней, используя весовые коэффициенты:
¼(1/2;1;1;1;1/2)
Для этого просуммируем уровень ряда последовательно за каждые 6 кварталов со сдвигами на один момент времени и определим условные годовые Yt. Разделив полученные суммы на 4 найдем скользящие средние. Полученные таким образом выровненные значения уже не сезонной содержат сезонной компоненты. Приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние.
Расчет оценок сезонной компоненты представлен в таблице:
t |
Y |
Центрированная скользящая средняя |
Оценка сезонных колебаний |
|
Yt |
Ŷt |
e=Y-Ŷ |
1 |
12,6 |
|
|
2 |
18,92 |
|
|
3 |
17,08 |
15,57 |
1,51 |
4 |
15,51 |
14,57 |
0,94 |
5 |
8,97 |
13,48 |
-4,51 |
6 |
14,52 |
12,62 |
1,90 |
7 |
12,77 |
11,88 |
0,89 |
8 |
12,96 |
11,02 |
1,94 |
9 |
5,55 |
10,15 |
-4,60 |
10 |
11,09 |
8,72 |
2,37 |
11 |
9,23 |
7,30 |
1,93 |
12 |
5,03 |
6,61 |
-1,58 |
13 |
2,15 |
6,19 |
-4,04 |
14 |
8,95 |
6,12 |
2,83 |
15 |
8,04 |
5,95 |
2,09 |
16 |
5,68 |
5,32 |
0,36 |
17 |
0,14 |
4,45 |
-4,31 |
18 |
5,85 |
3,58 |
2,27 |
19 |
4,21 |
3,18 |
1,03 |
20 |
2,56 |
2,93 |
-0,37 |
21 |
0,08 |
2,29 |
-2,21 |
22 |
3,87 |
1,69 |
2,18 |
23 |
1,1 |
|
|
24 |
0,85 |
|
|
Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и центрированными скользящими средними. Используем эти оценки для расчета значений сезонной компоненты S.Для этого найдем средние за каждый квартал оценки сезонной компоненты S.В моделях с сезонной компонентой предполагается, что сезонное воздействие за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равно 0. Для этого введем корректирующий коэффициент, который равен сумме всех средних значений.
Sj=еj-k
Сумма всех Sj=0
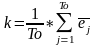
где k-коэффициент корректировки, равный 0,09
Sj - сезонная волна.
Таблица 7
|
Квартал |
|||
|
1 |
2 |
3 |
4 |
1 |
|
|
|
|
2 |
-4,51 |
1,90 |
0,89 |
1,94 |
3 |
-4,60 |
2,37 |
1,93 |
-1,58 |
4 |
-4,04 |
2,83 |
2,09 |
0,36 |
5 |
-4,31 |
2,27 |
1,03 |
-0,37 |
6 |
|
|
|
|
Всего за период |
-17,46 |
9,37 |
5,94 |
0,36 |
Средняя оценка сезонной компоненты |
-4,37 |
2,34 |
1,48 |
0,09 |
Скорректированная сезонная компонента |
-4,25 |
2,45 |
1,60 |
0,20 |
Коэффициент корректировки |
-0,11 |
|
|
|
Проведем десезонолизацию исходных данных, вычитая соответствующие значения сезонной компоненты из фактических значений, т.е.
Uij=yij-Sj
Вычисленные таким образом значения состоят из тренда и случайной компоненты.
Таблица 8
t |
Yt |
Si |
U=Yt-Si |
T |
ε=Yt-T-S |
ŷ=T+S |
1,00 |
12,6 |
-4,25 |
16,85 |
16,18 |
0,67 |
11,93 |
2,00 |
18,92 |
2,45 |
16,47 |
15,46 |
1,01 |
17,91 |
3,00 |
17,08 |
1,60 |
15,48 |
14,73 |
0,75 |
16,33 |
4,00 |
15,51 |
0,20 |
15,31 |
14,00 |
1,31 |
14,20 |
5,00 |
8,97 |
-4,25 |
13,22 |
13,28 |
-0,05 |
9,02 |
6,00 |
14,52 |
2,45 |
12,07 |
12,55 |
-0,48 |
15,00 |
7,00 |
12,77 |
1,60 |
11,17 |
11,82 |
-0,65 |
13,42 |
8,00 |
12,96 |
0,20 |
12,76 |
11,09 |
1,66 |
11,30 |
9,00 |
5,55 |
-4,25 |
9,80 |
10,37 |
-0,56 |
6,11 |
10,00 |
11,09 |
2,45 |
8,64 |
9,64 |
-1,00 |
12,09 |
11,00 |
9,23 |
1,60 |
7,63 |
8,91 |
-1,28 |
10,51 |
12,00 |
5,03 |
0,20 |
4,83 |
8,18 |
-3,36 |
8,39 |
13,00 |
2,15 |
-4,25 |
6,40 |
7,46 |
-1,05 |
3,20 |
14,00 |
8,95 |
2,45 |
6,50 |
6,73 |
-0,23 |
9,18 |
15,00 |
8,04 |
1,60 |
6,44 |
6,00 |
0,44 |
7,60 |
16,00 |
5,68 |
0,20 |
5,48 |
5,28 |
0,20 |
5,48 |
17,00 |
0,14 |
-4,25 |
4,39 |
4,55 |
-0,16 |
0,30 |
18,00 |
5,85 |
2,45 |
3,40 |
3,82 |
-0,43 |
6,28 |
19,00 |
4,21 |
1,60 |
2,61 |
3,09 |
-0,48 |
4,69 |
20,00 |
2,56 |
0,20 |
2,36 |
2,37 |
-0,01 |
2,57 |
21,00 |
0,08 |
-4,25 |
4,33 |
1,64 |
2,69 |
-2,61 |
22,00 |
3,87 |
2,45 |
1,42 |
0,91 |
0,50 |
3,37 |
23,00 |
1,1 |
1,60 |
-0,50 |
0,19 |
-0,68 |
1,78 |
24,00 |
0,85 |
0,20 |
0,65 |
-0,54 |
1,19 |
-0,34 |
Подбираем для полученного ряда кривую роста ,апроксимирующую тренд. Находим параметры уравнений кривой роста и подставляем значения t.Полученные оценки являются значениями тренда.
Определим компоненту Т данной модели. Для этого проведем аналитическое выравнивание ряда с помощью линейного тренда. Уравнение будет иметь вид:
y = -0,7272x + 16,911
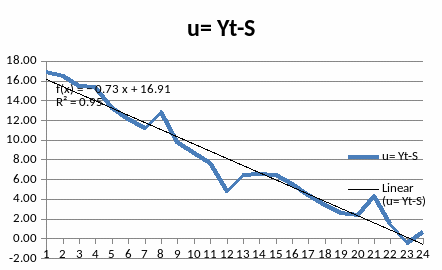
Рис. 4