Требуется:
1)построить автокорреляционную функцию до порядка n/3;
2)определить наличие во временном ряду сезонных колебаний;
3)построить модели: аддитивную, мультипликативную и модель Четверикова и проверить каждую на адекватность и точность;
4) выбрать лучшую модель и построить прогноз на 2 последующих шага;
Решение:
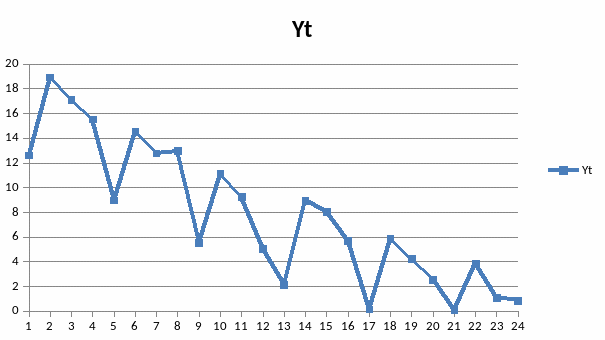
Исходные данные:
T |
Yt |
1 |
12,6 |
2 |
18,92 |
3 |
17,08 |
4 |
15,51 |
5 |
8,97 |
6 |
14,52 |
7 |
12,77 |
8 |
12,96 |
9 |
5,55 |
10 |
11,09 |
11 |
9,23 |
12 |
5,03 |
13 |
2,15 |
14 |
8,95 |
15 |
8,04 |
16 |
5,68 |
17 |
0,14 |
18 |
5,85 |
19 |
4,21 |
20 |
2,56 |
21 |
0,08 |
22 |
3,87 |
23 |
1,1 |
24 |
0,85 |
Построение автокорреляционной функции до порядка n/3
Построим автокорреляционную функцию с помощью функции КОРРЕЛ до 8 порядка включительно:
Таблица 2
Автокорреляционная ф-я |
||||||||
порядок |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
значение |
0,722925 |
0,655045 |
0,651933 |
0,945934 |
0,592986 |
0,539753 |
0,552501 |
0,916298 |
|
|
|
|
|
|
|
|
|
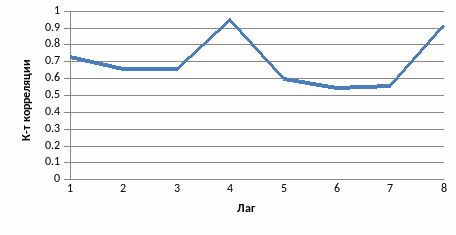
Рис.1
Наибольший коэффициент автокорреляции – r (4) . Следовательно, можно предположить, ряд содержит циклическую компоненту с периодом равным 4.
Корреляцию можно рассчитать и вручную.
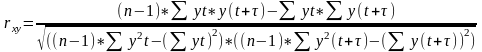
Автокорреляция |
|||||||||||
II |
yt |
y(t+τ) |
yt·y(t+τ) |
y²t |
y²(t+τ) |
I |
yt |
y(t+τ) |
yt·y(t+τ) |
y²t |
y²(t+τ) |
|
12,6 |
17,08 |
215,21 |
158,76 |
291,73 |
|
12,6 |
18,92 |
238,39 |
158,76 |
357,97 |
|
18,92 |
15,51 |
293,45 |
357,97 |
240,56 |
|
18,92 |
17,08 |
323,15 |
357,97 |
291,73 |
|
17,08 |
8,97 |
153,21 |
291,73 |
80,46 |
|
17,08 |
15,51 |
264,91 |
291,73 |
240,56 |
|
15,51 |
14,52 |
225,21 |
240,56 |
210,83 |
|
15,51 |
8,97 |
139,12 |
240,56 |
80,46 |
|
8,97 |
12,77 |
114,55 |
80,46 |
163,07 |
|
8,97 |
14,52 |
130,24 |
80,46 |
210,83 |
|
14,52 |
12,96 |
188,18 |
210,83 |
167,96 |
|
14,52 |
12,77 |
185,42 |
210,83 |
163,07 |
|
12,77 |
5,55 |
70,87 |
163,07 |
30,80 |
|
12,77 |
12,96 |
165,50 |
163,07 |
167,96 |
|
12,96 |
11,09 |
143,73 |
167,96 |
122,99 |
|
12,96 |
5,55 |
71,93 |
167,96 |
30,80 |
|
5,55 |
9,23 |
51,23 |
30,80 |
85,19 |
|
5,55 |
11,09 |
61,55 |
30,80 |
122,99 |
|
11,09 |
5,03 |
55,78 |
122,99 |
25,30 |
|
11,09 |
9,23 |
102,36 |
122,99 |
85,19 |
|
9,23 |
2,15 |
19,84 |
85,19 |
4,62 |
|
9,23 |
5,03 |
46,43 |
85,19 |
25,30 |
|
5,03 |
8,95 |
45,02 |
25,30 |
80,10 |
|
5,03 |
2,15 |
10,81 |
25,30 |
4,62 |
|
2,15 |
8,04 |
17,29 |
4,62 |
64,64 |
|
2,15 |
8,95 |
19,24 |
4,62 |
80,10 |
|
8,95 |
5,68 |
50,84 |
80,10 |
32,26 |
|
8,95 |
8,04 |
71,96 |
80,10 |
64,64 |
|
8,04 |
0,14 |
1,13 |
64,64 |
0,02 |
|
8,04 |
5,68 |
45,67 |
64,64 |
32,26 |
|
5,68 |
5,85 |
33,23 |
32,26 |
34,22 |
|
5,68 |
0,14 |
0,80 |
32,26 |
0,02 |
|
0,14 |
4,21 |
0,59 |
0,02 |
17,72 |
|
0,14 |
5,85 |
0,82 |
0,02 |
34,22 |
|
5,85 |
2,56 |
14,98 |
34,22 |
6,55 |
|
5,85 |
4,21 |
24,63 |
34,22 |
17,72 |
|
4,21 |
0,08 |
0,34 |
17,72 |
0,01 |
|
4,21 |
2,56 |
10,78 |
17,72 |
6,55 |
|
2,56 |
3,87 |
9,91 |
6,55 |
14,98 |
|
2,56 |
0,08 |
0,20 |
6,55 |
0,01 |
|
0,08 |
1,10 |
0,09 |
0,01 |
1,21 |
|
0,08 |
3,87 |
0,31 |
0,01 |
14,98 |
|
3,87 |
26,50 |
102,56 |
14,98 |
702,25 |
|
3,87 |
1,10 |
4,26 |
14,98 |
1,21 |
|
|
|
|
|
|
|
1,1 |
26,50 |
29,15 |
1,21 |
702,25 |
|
|
|
|
|
|
|
|
|
|
|
|
Сумма |
185,76 |
181,84 |
1807,20 |
2190,76 |
2377,49 |
|
186,86 |
200,76 |
1947,63 |
2191,97 |
2735,46 |
|
|
|
|
|
|
|
|
|
|
|
|
r(2) |
0,36846 |
|
|
|
|
|
r(1) |
0,388974 |
|
|
|
r(2) |
0,36846 |
|
|
|
|
|
r(1) |
0,388974 |
|
|
|