
- •1.Обобщенная паутинообразная модель
- •2. Обобщенная паутинообразная модель
- •3.Обобщенная паутинообразная модель
- •4.Статические функции спроса и предложения
- •5.Модель равновесия гэррода
- •6.Потребительское предпочтение…
- •7. Модель самуэльсона (Мультипликаторно-акселераторная)
- •8.Модель муза.
- •9. Модель самуєльсона с налогообложением(1)
- •10. Модель самуєльсона с налогообложением(1).
- •11. Модель хикса (взаимодействие мультипликатора и акселератора)
- •12.Модель хикса с внешней торговлей
- •13. Модель образования запасов мецлера
- •14.Модель взаимодействия двух открытых экономик.
- •16.Пропорциональная стабилизационная политика (1).
- •17.Пропорциональная стабилизационная политика (2).
- •18. Модель рыболовства
- •19. Упрощенная модель национальной экономики(1).
- •20. Упрощенная модель национальной экономики (2).
- •21. Модель вальраса регулирования цены
- •22. Динамическая кейнсианская модель
- •23.Модель динамики национальной экономики (1).
- •24. Модель динамики национальной экономики (2).
- •25. Модель подъемов и спадов нац эк
- •26. Модель национальной экономики.
23.Модель динамики национальной экономики (1).
Пусть Y(t) – национальный продукт, Ye(t) – ожидаемый объем национального продукта, B(t), Bd(t) – фактический и желаемый объем оборотного капитала.
Выпуск продукта регулируется в соответствии с расхождением между требуемым и действительным оборотным капиталом:
 ,
,
фактический оборотный капитал изменяется, если на рынке отсутствует равновесие:
 ,
,
где S(t), I(t) – сбережения и инвестиции соответственно.
Требуемый оборотный капитал линейно зависит от ожидаемого выпуска:
 .
.
Ожидаемый выпуск определяется с лагом s в соответствии с уравнением запаздывания:
 .
.
Накопление, инвестиции и выпуск связаны соотношением:
 .
.
Приведите модель к дифференциальному уравнению, определите состояния равновесия в модели и тип устойчивости равновесия.
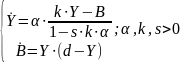
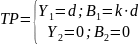
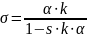



При s · k · α < 1 → σ > 0 (т.к. по условию α, k, s > 0, то числитель k · α > 0)→ ТР1, 2 неустойчивые (или седло, которое зависит от d: седло при Δ < 0)
При s · k · α > 1 → σ < 0 (т.к. по условию α, k, s > 0, то числитель k · α > 0)→ ТР1, 2 устойчивые (или седло, которое зависит от d: седло при Δ < 0)
Т.к. динамическая система не имеет вид: → ТР не дикритический узел
D ≥ 0 при α2 · k2 ≥ 4 · (± a · d) · (1 – s · k · α) (не выражается в явном виде, знаменатель D всегда положительный, т.к. 2-ая степень) → ТР седло или узел
При D = 0 → ТР вырожденный узел
В остальных случаях при D ≥ 0 ТР невырожденный узел
D < 0 при α2 · k2 < 4 · (± a · d) · (1 – s · k · α) (не выражается в явном виде) → ТР фокус или центр
Т.к. по условию α, k, s > 0, то σ ≠ 0 → ТР не центр (всегда есть действительная часть комплексного корня ≠ 0)
В остальных случаях при D < 0 ТР фокус
24. Модель динамики национальной экономики (2).
Пусть Y(t) – национальный продукт, Ye(t) – ожидаемый объем национального продукта, B(t), Bd(t) – фактический и желаемый объем оборотного капитала.
Выпуск продукта регулируется в соответствии с расхождением между требуемым и действительным оборотным капиталом:
 ,
,
фактический оборотный капитал изменяется, если на рынке отсутствует равновесие:
 ,
,
где S(t), I(t) – сбережения и инвестиции соответственно.
Требуемый оборотный капитал линейно зависит от ожидаемого выпуска:
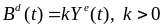 .
.
Ожидаемый выпуск определяется с лагом s в соответствии с уравнением запаздывания:
 .
.
Накопление, инвестиции и выпуск связаны соотношением:
 .
.
Приведите модель к дифференциальному уравнению, определите состояния равновесия в модели и тип устойчивости равновесия.
Из первых трёх уравнений следует что, модель может быть выражена одним уравнением

Используя ожидаемый выпуск данное уравнение преобразовывается к виду
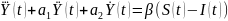
Где
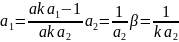
С
учитывая связь накопления, инвестиций
и выпуска и заменив переменные x=Y, y= ,
z=
,
z=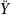 получим следующую систему уравнений
получим следующую систему уравнений
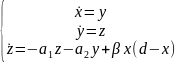
Анализ модели
В
точке равновесия
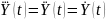 поэтому
поэтому

Таким образом матрица коэффициентов линеаризованной системы имеет вид

В первой точке равновесия (0,0,0) матрица коэффициентов линеаризованной системы имеет вид


Из
вида характеристического многочлена
получаем
 так как
так как
 для достаточно больших лямдаследовательно
характеристический многочлен должен
иметь хотябы один положительный корень.
Таким образом точка равновесия
неустойчива.
для достаточно больших лямдаследовательно
характеристический многочлен должен
иметь хотябы один положительный корень.
Таким образом точка равновесия
неустойчива.
Во второй точке равновесия (d,0,0) матрица коэффициентов линеаризованной системы имеет вид
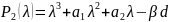
Теперь
для
 многочлен имеет положительные коэффициенты
и потому не
может иметь положительный действительный
корень.
многочлен имеет положительные коэффициенты
и потому не
может иметь положительный действительный
корень.
В
случае если
 то корни равны 0,
то корни равны 0,
 ,
,
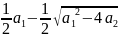 так как система не гиперболическая мы
не можем сделать заключение о природе
точек равновесия. Однако если
так как система не гиперболическая мы
не можем сделать заключение о природе
точек равновесия. Однако если
 мало и положительно то
мало и положительно то изменится изначально и останется близким
к 0 из за непрерывности многочлена
изменится изначально и останется близким
к 0 из за непрерывности многочлена
 .
В этом случае мы можем принебречь членами
.
В этом случае мы можем принебречь членами
 в
и
получим приблежонное значение
в
и
получим приблежонное значение
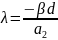
остальные собственные значения должны быть либо действительными и отрицательными либо комплексными с действительными частями приближенно равными -a1/2
таким образом точка равновесия (d,0,0) устойчива.
Корда
bd возрастает ( )
неустойчивость может возникнуть только
если действительные части комплексных
собственных значений станут положительными.
Следовательно действительные части
должны стать равными нулю при некоторых
критических значениях
)
неустойчивость может возникнуть только
если действительные части комплексных
собственных значений станут положительными.
Следовательно действительные части
должны стать равными нулю при некоторых
критических значениях
Так
как при критических значениях

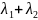 =0,
=0,

Подставляя в характеристический многочлен получим

Отсюда

Для значений параметров таких что меньше критической величины, точка равновесия будет устойчива и, таким образом траектории через определённый период будут притягиваться к точке равновесия.
