10. Модель самуєльсона с налогообложением(1).

Предположим, что потребление – это лаговая функция чистого дохода, т.е.

C_t = bY^d_t-1, 0<b<1,

где Y^d_t = Y_t – T_t – чистый доход; b – предельная склонность к потреблению;

T_t = Y_t – налоги,  – фиксированная ставка налога (0<<1).

Функция инвестирования

I_t=I_t'+I_t",

включает вынужденное инвестирование – I_t' и государственные расходы, которые составляют все налоговые поступления плюс некоторую фиксированную величину: I_t" = T_t+G. Вынужденное инвестирование зависит от изменений спроса на товары потребления в соответствии с принципом акселерации:

I_t'=k(C_t–C_t-1),

где k – коэффициент акселерации.

Условие равновесия модели:

Y_t=C_t+I_t.

Определите характер равновесия в зависимости от соотношения параметров b, k и  модели.

Предположим, что существует лаг между получением налогов и расходованием средств, т.е. I_t" = G+T_t-i.

Какие изменения произойдут в условиях устойчивости равновесия модели?

11. Модель хикса (взаимодействие мультипликатора и акселератора)

Рассмотрим модель взаимодействия мультипликатора и акселератора следующего вида:

где Y_t – национальный доход; С_t – потребление; I_t – инвестирование; I"_t – автономное инвестирование, растущее с постоянным темпом g; I'_t – вынужденное инвестирование, которое определяется с лагом в один период.

Найдите равновесное состоянием равновесия для дохода и определите условия его устойчивости.

Подстановкой преобразовываем начальные условия к виду:

λ1* λ2=k

12.Модель хикса с внешней торговлей

Рассмотрим модель взаимодействия мультипликатора и акселератора следующего вида:

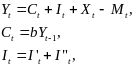
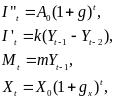
где Y_t – национальный доход; С_t – потребление; I_t – инвестирование; I"_t – автономное инвестирование, растущее с постоянным темпом g; I'_t – вынужденное инвестирование, которое определяется с лагом в один период; M_t – импорт является функцией дохода с лагом в один период; X_t – экспорт определяется внешним спросом и растет с постоянным темпом g_x.

Найдите равновесное состоянием равновесия для дохода и определите условия его устойчивости.

Как изменятся условия устойчивости в случае, если импорт будет определяться текущим уровнем потребления и инвестиционного спроса, т.е.

M_t = m₁C_t + m₂I_t, 0<m₁<1, 0<m₂<1 ?

_Если M_t = m₁C_t + m₂I_t, 0<m₁<1, 0<m₂<1 ?

13. Модель образования запасов мецлера

Текущий уровень производства равен сумме уровней производства товаров потребления и инвестиционных товаров. Уровень производства состоит из двух компонент: объема продукции, который продан в настоящий момент времени в оответствии с ожидаемым уровнем продаж производителей (U_t) и объема продукции, переводящей уровень запасов на желаемый уровень (Q^*_t). Реальный уровень продаж совпадает с текущим уровнем потребительского спроса C_t. Основное соотношение модели имеет вид:

Y_t = U_t + (Q^*_t – Q_t-1) + I₀,

где Y_t – уровень дохода;

I₀ – экзогенное инвестирование;

Q_t – текущий уровень запаса;

Q^*_t – желаемый уровень запаса, который определяется из условия постоянства соотношения между уровнем продаж и уровнем запаса:

Q^*_t = kU_t,

k – акселератор образования запасов.

Ожидаемый уровень продаж связан с уровнем реализованных продаж экстраполяционным механизмом:

U_t = C_t-1 + (C_t-1–C_t-2), >0.

Потребительский спрос зависит от текущего дохода, т.е.

C_t = bY_t.

В любом периоде уровень запаса Q_t равен тому уровню, который производители спланировали для этого периода (Q^*_t) за вычетом непредвиденных изменений уровня запасов (C_t – U_t).

Определите условия устойчивости модели в зависимости от параметра .

Решение

Частное решение получается в виде Yt=Y, константы, которая дает следующее решение:

Данная точка является стационарной точкой равновесия, которая задана мультипликатором и константой экзогенных расходов.

Характеристическое уравнение для однородной части, соответствующее уравнению:

λ³-b[(1+k)(1+p)+1] λ²+b(1+k)(1+2p) λ-(1+k)bp=0

Применяя условия стабильности имеем:

1-b[(1+k)(1+p)+1]+b(1+k)(1+2p) -(1+k)bp>0

1+b[(1+k)(1+p)+1]+b(1+k)(1+2p) +(1+k)bp>0

1-b[(1+k)(1+p)+1]-b(1+k)(1+2p) +3(1+k)bp>0

-(1+k)²b²p²+ b²(1+k)p[(1+k)(1+p)+1]-b(1+k)(1+2p)+1>0

Первое и второе неравенства выполняются, поскольку предельная склонность к потреблению <1, а коэффициент ожиданий неотрицателен. Существенными неравенствами являются третье и четвертое, которые после простых преобразований можно представить как:

3-b(2k+3)>0

(1+k)(2+k)pb² –(1+k)(1+2p)b+1>0

Для р=0 критическим условие стабильности становится b<1/(1+k), то есть все комбинации b, k лежащие под кривой b=1/(1+k). При р=0 можно сказать, что производители зафиксировали свои ожидания, то есть ожидаемый уровень продаж совпадает с реализованным уровнем продаж. Для р=1 область стабильности становится меньшей и таким, что экономическая система вероятней всего становится не стабильной.