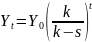Y
1.ОБОБЩЕННАЯ ПАУТИНООБРАЗНАЯ МОДЕЛЬ 3
2. ОБОБЩЕННАЯ ПАУТИНООБРАЗНАЯ МОДЕЛЬ 6
3.ОБОБЩЕННАЯ ПАУТИНООБРАЗНАЯ МОДЕЛЬ 8
4.СТАТИЧЕСКИЕ ФУНКЦИИ СПРОСА И ПРЕДЛОЖЕНИЯ 10
5.МОДЕЛЬ РАВНОВЕСИЯ ГЭРРОДА 11
7. МОДЕЛЬ САМУЭЛЬСОНА (Мультипликаторно-акселераторная) 14
8.МОДЕЛЬ МУЗА. 16
9. МОДЕЛЬ САМУЄЛЬСОНА С НАЛОГООБЛОЖЕНИЕМ(1) 18
10. МОДЕЛЬ САМУЄЛЬСОНА С НАЛОГООБЛОЖЕНИЕМ(1). 21
11. МОДЕЛЬ ХИКСА (взаимодействие мультипликатора и акселератора) 22
12.МОДЕЛЬ ХИКСА С ВНЕШНЕЙ ТОРГОВЛЕЙ 24
13. МОДЕЛЬ ОБРАЗОВАНИЯ ЗАПАСОВ МЕЦЛЕРА 26
14.Модель взаимодействия двух открытых экономик. 29
16.ПРОПОРЦИОНАЛЬНАЯ СТАБИЛИЗАЦИОННАЯ ПОЛИТИКА (1). 30
17.ПРОПОРЦИОНАЛЬНАЯ СТАБИЛИЗАЦИОННАЯ ПОЛИТИКА (2). 33
18. МОДЕЛЬ РЫБОЛОВСТВА 35
36
19. УПРОЩЕННАЯ МОДЕЛЬ НАЦИОНАЛЬНОЙ ЭКОНОМИКИ(1). 37
20. УПРОЩЕННАЯ МОДЕЛЬ НАЦИОНАЛЬНОЙ ЭКОНОМИКИ (2). 39
21. МОДЕЛЬ ВАЛЬРАСА РЕГУЛИРОВАНИЯ ЦЕНЫ 41
22. ДИНАМИЧЕСКАЯ КЕЙНСИАНСКАЯ МОДЕЛЬ 43
23.МОДЕЛЬ ДИНАМИКИ НАЦИОНАЛЬНОЙ ЭКОНОМИКИ (1). 45
24. МОДЕЛЬ ДИНАМИКИ НАЦИОНАЛЬНОЙ ЭКОНОМИКИ (2). 47
25. МОДЕЛЬ ПОДЪЕМОВ И СПАДОВ НАЦ ЭК 51
26. МОДЕЛЬ НАЦИОНАЛЬНОЙ ЭКОНОМИКИ. 53
1.Обобщенная паутинообразная модель
Найдите условие устойчивости цены равновесия в этом случае и покажите, как меняются темп и характер поведения паутинообразной модели по сравнению с частным случаем использования в качестве ожидаемой цены предыдущего периода.
РЕШЕНИЕ
Dt = a+bpt
St = a1+b1 pte
Условие равновесия:
Dt = St
a+bpt = a1+b1 pte
bpt – b1 pte = a1 – a
Характеристическое уравнение:
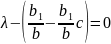
Общее решение:
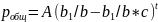
Следовательно, система будет стремится к устойчивому равновесию, при b>b1(1-c)
Частное решение:
pчастt = С
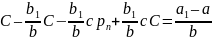
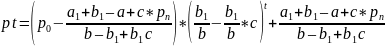
Равновесие будет устойчивым при b>b1(1-c)
При использовании цены предыдущего периода:
Условие равновесия:
a+bpt = a1+b1pt-1
bpt – b1 pt-1 = a1 – a
Решение: pt = pобщt + pчастt
Однородное уравнение:
Характеристическое уравнение:
Общее решение :
pобщt = Alt
Частное решение:
pчастt = С
a+bС = a1+b1С
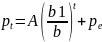
Из начальных условий p(0)=p0:
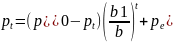
При |b1|<|b| - амплитуда колебаний уменьшается – устойчивое равновесие
В паутинообразной модели точка равновесия является устойчивой, если угол наклона кривой спроса больше чем угол наклона кривой предложения.
2. Обобщенная паутинообразная модель
Найдите цену равновесия и условие устойчивости в этом случае и покажите, как меняются темп и характер поведения паутинообразной модели при различных значениях
РЕШЕНИЕ
Dt = a+bpt
St = a1+b1 pte
Условие равновесия:
Dt = St
a+bpt = a1+b1 pte
bpt – b1 pte = a1 – a
Характеристическое уравнение:
Общее решение:
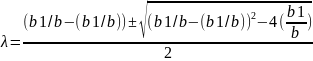
Для выполнения условия устойчивости достаточно, чтобы произведение кореней – (b1/b)<1!
Условие действительности корней
3.Обобщенная паутинообразная модель
Найдите условие устойчивости цены равновесия в этом случае и покажите, как меняются темп и характер поведения паутинообразной модели в зависимости от значения параметра .
РЕШЕНИЕ
Dt = a+bpt
St = a1+b1 pte
Условие равновесия:
Dt = St
a+bpt = a1+b1 pte
bpt – b1 pte = a1 – a
Характеристическое уравнение:
Общее решение:
Следовательно, система будет стремится к устойчивому равновесию, при b>b1(1-)
Частное решение:
pчастt = С
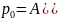
Равновесие будет устойчивым при b>b1(1-)
4.Статические функции спроса и предложения
где – чувствительность цены к возникновению избыточного спроса, проведите анализ устойчивости статической равновесной точки паутинообразной модели.
В точке равновесия De=Se, p=pe
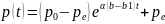
АСИМПТОТИЧЕСКАЯ УСТОЙЧИВОСТЬ. Если при увеличении t p(t)->pe
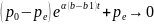
5.Модель равновесия гэррода
где St – ожидаемое накопление, s – склонность к накоплению;
It – ожидаемое инвестирование, k – акселератор;
Yt – национальный доход.
Опишите динамику дохода в данной модели. Покажите, как изменится решение модели в случае, если накопление пропорционально текущему уровню дохода (St=sYt), а функция инвестирования останется неизменной. Какие условия должны выполняться для обеспечения устойчивого роста в модели?
РЕШЕНИЕ:
Характеристическое уравнение:
,
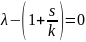
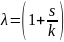
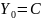
Динамика дохода с акселератором:
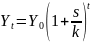
(St=sYt):
Характеристическое уравнение:
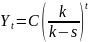
Динамика дохода с акселератором:
