Угловой коэффициент. Наклон функции

О наклоне линейной функции у = ах + b, судят по её угловому коэффициенту = числу а.

Говорят, что функция положительно наклонена к положительному направлению оси ОХ, если a>0 (угол острый) и отрицательно наклонена к оси ОХ при а < 0 (угол тупой). (Рис.8.) При а=0 прямая совпадает с осью ОХ или будет ей параллельна.

Для линейной функции число можно найти как tg угла , то есть а = tg .(Рис.8.)

Если функция положительно наклонена, то говорят о положительной, или прямой зависимости между двумя величинами. То есть, обе величины или возрастают или убывают – изменяются в одном направлении. Например, цена и предложение имеют прямую зависимость. При увеличении цены предложение тоже увеличивается.

Если функция наклонена отрицательно, то говоря об обратной зависимости между двумя величинами. Если одна величина растёт, то другая – убывает. Например цена и спрос. Если цена растёт, то спрос – падает.

Рис.8.

Производная функции и эластичность

Производная показывает, как изменяется зависимая переменная при изменении независимой. Если, например, производная некоторой функции равна 2, это означает, что при изменении независимой переменной на некоторую величину зависимая изменится на величину в два раза большую.

В отличие от производной, которая широко используется в самых разных научных дисциплинах, эластичность практически не выходит за пределы экономики. Именно поэтому ее знают гораздо хуже и, более того, часто путают с производной. Как мы увидим ниже, эластичность связана с производной, но не более.

Эластичность есть мера изменения зависимой переменной в ответ на изменение независимой переменной.

На первый взгляд, определение практически тождественно определению производной. Есть однако, одно очень важное отличие. Производная показывает, соотношение между тем, на какую величину изменились зависимая и независимая переменная. Эластичность же показывает соотношение между тем, во сколько раз (или на сколько процентов) изменились зависимая и независимая переменная.

В экономике исходные функции часто называют "полными", а их производные – "предельными".

Например, производную функции полной полезности называют предельной полезностью, а производную функции полных издержек – предельными издержками.

Производная и эластичность линейной функции

Линейная функция имеет вид y = ax + b, где x – независимая переменная, y – зависимая переменная, а a и b – постоянные величины (константы). А значит, на сколько бы не менялся x, y всегда будет меняться на величину, в a раз большую. То есть, величина a и будет значением производной.

При изменении независимой переменной x на некоторую величину ∆x – приращение или смещение аргумента (читается "дельта икс") зависимая переменная y изменяется на величину ∆y – приращение или смещение функции (читается "дельта игрек"). Где бы не располагался интервал ∆x, величина ∆y всегда будет одной и той же. (Рис. 9.)

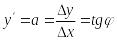
y' – символ, который обозначает производную функцию y (читается "игрек-штрих").

Рис. 9.

Теперь вернёмся к эластичности. По определению эластичность вычисляется по формуле:

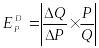, так как мы уже говорили о том, что спрос это функция от цены, то выражение

- производная линейной функции. Тогда формула эластичности будет выглядеть так: