5. Основные свойства систем управления для физических, производственных и социально-экономических объектов и процессов. Управляемость и наблюдаемость.

Для многих систем, представленных в форме пространства состояний, эти понятия позволяют решать задачи о переводе объекта из одного состояния в другое, а также определение информации о его переменных состояний за конечное время. Управляемость Управляемость – это свойство объекта управления переходить из заданной начальной точки в заданную конечную точку за конечный интервал времени. Для линейных стационарных систем это свойство может быть определено следующим образом: Пусть линейная стационарная система задана уравнением вида: 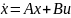, где Aи B– матрицы коэффициентов соответственно при векторах состояния и управления, причем 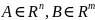. 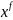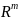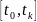Тогда система называется вполне управляемой, если для любой точки из существует допустимое управление на конечном интервале времени , переводящее систему из точки в точку , или если для любой точки существует допустимое управление на конечном интервале времени , переводящее систему из состояния 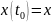в состояние 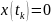. Критерий управляемости. ПустьАи В постоянны. Рассмотрим матрицу управляемости: 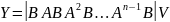Она состоит из столбцов матрицыВи произведений матриц и имеет размерность nxn, тогда система вполне управляема тогда и только тогда, когда ранг матрицы управляемости равен n. Наблюдаемость. Наблюдаемость – свойство системы, когда по выходу переменных состояния можно полностью восстановить информацию о состоянии системы. 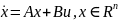Рассмотрим линейную стационарную систему Тогда система вполне или полностью наблюдаема, если существует такое 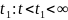, что по данным измерения y(τ) и u(τ) на интервале t<τ<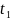 , можно определить состояние x(t). Полная наблюдаемость предлагает возможным определить x(t) по будущим значениям y(t) Введем матрицу наблюдаемости: 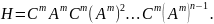Эта матрица состоит из транспонированной матрицы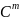 и ее произведений на матрицы 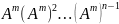и имеет размерность (nxnp). Тогда критерием полной наблюдаемости системы является равенство ранга матрицы числу n.

5. Основные свойства систем управления для физических, производственных и социально-экономических объектов и процессов. Устойчивость и чувствительность.

Под устойчивостью понимается способность динамической системы возвращаться в равновесное состояние после окончания действия возмущения, нарушившего это равновесие. Неустойчивая система после воздействия возмущения удаляется от равновесного состояния или начинает совершать вокруг него колебания с нарастающей амплитудой. Устойчивость линейной системы определяется не характером возмущения, а структурой самой системы. Говорят, что система устойчива "в малом", если определен факт наличия устойчивости, но не определены ее границы. Система устойчива "в большом", когда определены границы устойчивости и то, что реальные отклонения не выходят за эти границы. Соответственно, и задача исследования систем на устойчивость может быть поставлена двояко: 1) устойчива ли система при заданном значении ее параметров; 2) в каких диапазонах можно изменять параметры системы, не нарушая ее устойчивости Если система описывается линейным дифференциальным уравнением, то ее устойчивость не зависит от величины возмущения. Линейная система, устойчивая при малых возмущениях, будет устойчива и при больших. Нелинейные системы могут быть устойчивы при малых возмущениях и неустойчивы при больших. Чувствительность – изменение статических и динамических характеристик под действием внешних условий, приводящих к изменению параметров звена или системы. Влияние среды на систему может привести к изменению операторов преобразования W(s), что приводит к возникновению систем с переменной структурой (нестационарные системы). Если изменение операторов преобразования во времени много медленнее собственных и вынужденных процессов, то говорят о квазистационарности (т.е. параметры системы изменяются очень медленно). Для систем управления важно, чтобы малые операторы вариации операторов не приводили к большим изменениям свойств системы в целом. Работоспособная система управления должна быть инвариантной к возмущениям и устойчивой. Количественно чувствительность применительно к динамическим процессам определяют функциями чувствительности, представляющие собой частные производные от координаты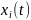 по исследованию параметру :
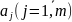