
- •1.Основные разделы теории управления для решения производственных и социально-экономических задач.
- •2.Место теории менеджмента в теории управления.
- •3.Особенности применения теории управления для физических, производственных и социально-экономических объектов и процессов.
- •4. Понятие управления по отклонению и по возмущению для физических, производственных и социально-экономических объектов и процессов.
- •Разомкнутые и замкнутые системы управления для физических, производственных и социально-экономических объектов и процессов.
- •Обратная связь при управлении для физических, производственных и социально-экономических объектов и процессов.
- •Стратегия и тактика управления для физических, производственных и социально-экономических объектов и процессов.
- •Организационные структуры управления для физических, производственных и социально-экономических объектов и процессов.
- •Информационная составляющая процессов управления для физических, производственных и социально-экономических объектов и процессов.
- •Методы описания процессов управления для физических, производственных и социально-экономических объектов и процессов.
- •Основные свойства систем управления для физических, производственных и социально-экономических объектов и процессов. Управляемость и наблюдаемость.
- •Основные свойства систем управления для физических, производственных и социально-экономических объектов и процессов. Устойчивость и чувствительность.
- •Оптимальное управление для физических, производственных и социально-экономических объектов и процессов. Критерии оптимизации.
- •Оптимальное управление для физических, производственных и социально-экономических объектов и процессов. Методы оптимизации.
- •Передаточная функция, типовые схемы и элементы систем управления для физических, производственных и социально-экономических объектов и процессов.
- •Принципы регулирования и стабилизации для физических, производственных и социально-экономических объектов и процессов.
- •Принципы инвариантности и автономности для физических, производственных и социально-экономических объектов и процессов.
- •Линейное программирование в задачах управления для физических, производственных и социально-экономических объектов и процессов. Транспортная задача.
- •Линейное программирование в задачах управления для физических, производственных и социально-экономических объектов и процессов. Долгосрочное планирование.
- •Линейное программирование в задачах управления для физических, производственных и социально-экономических объектов и процессов. Распределение ресурсов.
- •Исследование операций в задачах управления для физических, производственных и социально-экономических объектов и процессов. «Задача коммивояжера».
- •Исследование операций в задачах управления для физических, производственных и социально-экономических объектов и процессов. «Задача о ранце».
- •24. Исследование операций в задачах управления для физических, производственных и социально-экономических объектов и процессов. «Задача упаковки в контейнеры».
- •Элементы теории игр в задачах управления для физических, производственных и социально-экономических объектов и процессов. Примеры.
- •Элементы теории игр в задачах управления для физических, производственных и социально-экономических объектов и процессов. Стратегия и тактика.
- •Методы планирования эксперимента для физических, производственных и социально-экономических объектов и процессов.
- •Фильтрация и прогнозирование. Построение линии тренда и интерполяция информации для физических, производственных и социально-экономических объектов и процессов.
- •Кибернетика как раздел теории управления.
- •Технические средства управления, обработки и передачи информации для физических, производственных и социально-экономических объектов и процессов.
- •Адаптивные системы управления для физических, производственных и социально-экономических объектов и процессов.
- •Самонастраивающиеся системы управления для физических, производственных и социально-экономических объектов и процессов.
- •Самоорганизующиеся системы управления для физических, производственных и социально-экономических объектов и процессов.
- •Системы управления с прогнозированием для физических, производственных и социально-экономических объектов и процессов.
- •Современные теории управления. Эволюция и достижения теории управления как науки.
- •Методы учета «человеческого фактора» в теории управления.
- •Основные разделы теории управления для решения производственных и социально-экономических задач.
- •Место теории менеджмента в теории управления.
- •Основные разделы теории управления для решения производственных и социально-экономических задач.
- •Место теории менеджмента в теории управления.
Линейное программирование в задачах управления для физических, производственных и социально-экономических объектов и процессов. Распределение ресурсов.
Линейное программирование — раздел математического программирования, применяемый при разработке методов отыскания экстремума линейных функций нескольких переменных при линейных дополнительных ограничениях, налагаемых на переменные. По типу решаемых задач его методы разделяются на универсальные и специальные. С помощью универсальных методов могут решаться любые задачи линейного программирования (ЗЛП). Специальные методы учитывают особенности модели задачи, ее целевой функции и системы ограничений. Особенностью задач линейного программирования является то, что экстремума целевая функция достигает на границе области допустимых решений. Классические же методы дифференциального исчисления связаны с нахождением экстремумов функции во внутренней точке области допустимых значений. Отсюда — необходимость разработки новых методов.
Задачами линейного программирования (ЛП) называются задачи, в которых линейны как целевая функция, так и ограничения в виде равенств и неравенств и для которых методы математического анализа оказываются непригодными. ЛП представляет собой наиболее часто используемый метод оптимизации. В сфере лесного комплекса к их числу относятся задачи:
рациональное использование сырья и материалов; задачи оптимизации раскроя;
оптимизации производственной программы предприятий;
оптимального размещения и концентрации производства;
на составление оптимального плана перевозок, работы транспорта;
управления производственными запасами;
и многие другие, принадлежащие сфере оптимального планирования.
Формы записи задачи линейного программирования: Общей задачей линейного программирования называют задачу (2.1) при ограничениях (2.2) (2.3) (2.4) (2.5) -произвольные (2.6) где - заданные действительные числа; (2.1) – целевая функция; (2.1) – (2.6)–ограничения; -план задачи.
Оптимальное
распределение взаимозаменяемых
ресурсов.
Имеются m видов взаимозаменяемых
ресурсов а1,
а2,
., аm,
используемых при выполнении nразличных
работ (задач). Объемы работ, которые
должны быть выполнены, составляют b1,
b2,
. , bi,
bn единиц.
Заданы числа ![]() ,
указывающие, сколько единиц j -й
работы можно получить из единицы і -го
ресурса, а также Cij -
затраты на производство j -й работы
из единицы i -го ресурса. Требуется
распределить ресурсы по работам таким
образом, чтобы суммарная эффективность
выполненных работ была максимальной
(или суммарные затраты - минимальными).
,
указывающие, сколько единиц j -й
работы можно получить из единицы і -го
ресурса, а также Cij -
затраты на производство j -й работы
из единицы i -го ресурса. Требуется
распределить ресурсы по работам таким
образом, чтобы суммарная эффективность
выполненных работ была максимальной
(или суммарные затраты - минимальными).
Данная задача называется общей распределительной задачей. Количество единиц i -го ресурса, которое выделено на выполнение работ j -го вида, обозначим через xij.
Математическая модель рассматриваемой задачи такова:
|
(3.3) |
при ограничениях
|
(3.4) |
|
|
(3.5) |
|
Ограничение (3.4) означает, что план всех работ должен быть выполнен полностью, а (3.5) означает, что ресурсы должны быть израсходованы целиком.

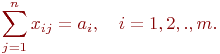 (3.5)
(3.5)