6.Неперервні випадкові величини.

Неперервною випадковою величиною називається така величина, всі можливі значення якої заповнюють суцільно деякий проміжок числової прямої. Випадкова величина називається неперервною, якщо її функцію розподілу можна подати у вигляді

,

де f(x) — невід’ємна функція, що задовольняє умову

.

7. Щільність розподілу. Властивості щільності розподілу.

Функція f(x) називається щільністю розподілу ймовірностей.

Зокрема, якщо F(x) диференційовна при всіх х і похідна її обмежена, то має місце рівність

.

Ймовірнісний зміст щільності розподілу наступний

.

З формули випливає, що ймовірність знаходження випадкової величини в проміжку (на відрізку) [x₁, x₂] можна знайти так:

Нехай є неперервна випадкова величина з неперервною та диференційованою функцією розподілу. Густиною ймовірності називається похідна від функції розподілу випадкової величини. Функція характеризує щільність, з якою розподіляються значення випадкової величини в даній точці. Інколи називають диференціальною функцією розподілу, або диференціальним законом розподілу.

Терміни “щільність розподілу” або “щільність ймовірності” особливо показові при вживанні механічної інтерпретації розподілу. Тобто, буквально характеризує щільність розподілу маси по , так звану лінійну щільність. Крива, що відображає щільність розподілу випадкової величини, називається кривою розподілу.

Властивості

• 

• 

• , де   — характеристична функція випадкової величини ξ.

(Варіант властивостей, що приведений нижче взятий з його книги)

8. Функція розподілу. Властивості функції розподілу.

Функція розподілу ймовірностей — В теорії ймовірностей це функція, яка повністю описує розподіл ймовірностей випадкової величини.

Нехай   — ймовірнісний простір, в якому   — множина елементарних подій,   — сукупність підмножин  , що утворюють  -алгебру, множини з  називаються випадковими подіями,   — міра на  , що задовольняє умову  . Функція  , визначена   рівністю

,

називається функцією розподілу ймовірностей або кумулятивною функцією розподілу ймовірностей випадкової величини ξ. Вираз в правій частині рівності є ймовірністю того, що випадкова величина   набуває значень менших або рівних  .

9.Функція розподілу дискретної випадкової величини.

 Функція розподілу ймовірностей дискретної випадкової величини та її властивості

 

Розглянемо функцію  , визначену на всій числовій осі   Для кожного   значення   дорівнює ймовірності того, що дискретна випадкова величина   приймає значення менші 

Тобто  .

Ця функція називається функцією розподілу ймовірностей (the probability distribution function), абофункцією розподілу.

Приклад.

Випадкова величина   ‑ число очок, що випали при однократному киданні грального кубика.

Ряд розподілу має вигляд:

Знайти функцію розподілу  . При    , тому що   не приймає значень менше 1.

якщо:  , то  ;

, то ;

,то ;

Далі аналогічно :            ;

;

.

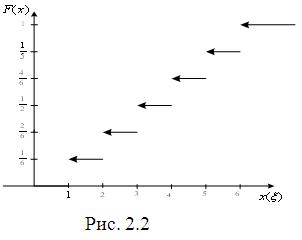
Знаючи функцію розподілу   (рис. 2.2), легко знайти імовірність того, що випадкова величина  задовольняє нерівності  .

З теореми про суму подій і ймовірностей одержимо:

;

.

За визначенням функції розподілу

.

Імовірність попадання дискретної випадкової величини в інтервал  дорівнює приросту (the growth) функції розподілу на цьому інтервалі.

Розглянемо основні властивості функції розподілу.

1. Функція розподілу є неспадною.

Нехай  ,  . Із знайденої формули отримаємо:

.

2. Значення функції задовольняють нерівність:

;

, це випливає з означення функції  .

3. Імовірність того, що дискретна випадкова величина   приймає одне із можливих значень  , дорівнює стрибку функції розподілу в точці 

Цю властивість наочно видно з наведеного вище прикладу.