
- •Класичне означення імовірності. Частота та ймовірність подій.
- •2)Властивості ймовірності.
- •3) Геометрична ймовірність.
- •4) Задача про зустріч.
- •6.Неперервні випадкові величини.
- •7. Щільність розподілу. Властивості щільності розподілу.
- •8. Функція розподілу. Властивості функції розподілу.
- •9.Функція розподілу дискретної випадкової величини.
- •10. Елементи комбінаторики.
- •1.3. Перестановки, сполучення, розміщення
- •11. Схема Бернуллі. Біноміальний розподіл. Характеристики біноміального розподілу.
- •Пояснення
- •12. Рівномірний розподіл. Характеристики рівномірного розподілу.
- •12) Нормальний розподіл.
- •14. Математичне сподівання неперервної випадкової величини.
- •15. Математичне сподівання дискретної випадкової величини.
- •16. Дисперсія випадкової величини. Властивості дисперсії.
- •18. Коефіцієнт кореляції.
- •22. Вибіркове середнє. Вибіркова дисперсія. Властивості вибіркового середнього та вибіркової дисперсії
- •23. Вибірковий коефіцієнт кореляції. Властивості вибіркового коефіцієнту кореляції
- •24. Довірче оцінювання. Інтервал довіри. Рівень довіри
- •25. Побудова інтервалу довіри для математичного сподівання нормального розподілу при відомій дисперсії
- •26. Побудова інтервалу довіри для математичного сподівання нормального розподілу при невідомій дисперсії
- •27. Побудова інтервалу довіри для дисперсії нормального розподілу
- •29 Основні поняття і методи регресійного аналізу
- •30 Метод найменших квадратів
- •32. Задача перевірки статистичних гіпотез. Критерій згоди про вигляд розподілу.
- •33. Критерій згоди Пірсона
26. Побудова інтервалу довіри для математичного сподівання нормального розподілу при невідомій дисперсії
Нехай тепер випадкова величина Х генеральної сукупності розподілена нормально, але середнє квадратичне відхилення невідоме. Потрібно оцінити невідоме математичне сподівання з допомогою довірчих інтервалів
Перш
ніж розв’язувати цю задачу, введемо
деякі поняття. Незалежні умови, що
накладаються на ni (чи Wi), називаються
в’язами. Наприклад,
 - тобто вимога того, щоб співпадали
теоретичні та вибіркові значення
середнього арифметичного та дисперсії
і т.д. Різниця між числом інтервалів
- тобто вимога того, щоб співпадали
теоретичні та вибіркові значення
середнього арифметичного та дисперсії
і т.д. Різниця між числом інтервалів
![]() та числом в’язей називається числом
ступенів вільності k=n-r, де r – число
в’язей.
та числом в’язей називається числом
ступенів вільності k=n-r, де r – число
в’язей.
Отже,
користуючись розподілом Стьюдента,
можна знайти довірчий інтервал:
![]()
що
накриває параметр m з надійністю
.
Тут
та S шукається по вибірці, а по таблиці
3 (див. додаток) по заданих n можна знайти
![]() .
.
Приклад
2. вибіркове обслідування прибутків за
місяць підприємців дало результати,
дані яких записані у вигляді розподілу:

Побудувати інтервал довір’я для математичного сподівання m, допустивши, що генеральна сукупність Х розподілена нормально з надійністю .
Рішення.
Обчислимо
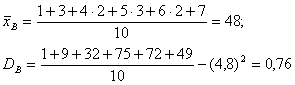
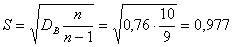
.За
надійністю
і числом ступенів вільності k=10-1=9 за
таблицею 3 знаходимо
![]() .
Тоді згідно формули (2):
.
Тоді згідно формули (2):

27. Побудова інтервалу довіри для дисперсії нормального розподілу
Доверительный интервал для дисперсии. Интервал Iγ для дисперсии
случайной
величины X
с
неизвестным законом распределения
имеет вид

где
zγ=arg
Φ
(
 )
-
значение аргумента функции Лапласа,
т.е. Ф(zγ)
=
)
-
значение аргумента функции Лапласа,
т.е. Ф(zγ)
=
Если случайная величина X распределена по нормальному закону с
параметрами
mx
и
σx
,
то величина
 распределена по закону χ
2
распределена по закону χ
2
с (n – 1) степенью свободы и доверительный интервал с надежностью γ для
дисперсии
имеет вид

 значения,
взятые из таблицы распределения χ
2
значения,
взятые из таблицы распределения χ
2
Формулы можно использовать при любом объеме выборки
n, так как эти интервалы Iγ построены на основе знания точных законов
распределения величин, связывающих Q и ˆQ
29 Основні поняття і методи регресійного аналізу
На
відміну від кореляційного аналізу, який
досліджує наявність і характер зв’язків
між випадковими величинами
![]() і Y
– ознаками генеральної сукупності,
регресійний аналіз встановлює аналітичну
форму цієї залежності.
і Y
– ознаками генеральної сукупності,
регресійний аналіз встановлює аналітичну
форму цієї залежності.
Якщо
 то
і
то
і
![]() – корельовані випадкові величини. Із
наближенням величини
– корельовані випадкові величини. Із
наближенням величини
![]() до одиниці залежність між цими випадковими
величинами наближається до лінійної
залежності вигляду
до одиниці залежність між цими випадковими
величинами наближається до лінійної
залежності вигляду
![]()
Як відомо, рівняння лінійної регресії на має вигляд:
![]() (3.40)
(3.40)
де 
 (3.41)
(3.41)
Вибірковим
рівнянням лінійної регресії
 на
на
 називається рівняння (3.40), якщо коефіцієнти
в ньому вибрано у вигляді точкових
оцінок
називається рівняння (3.40), якщо коефіцієнти
в ньому вибрано у вигляді точкових
оцінок
 і
і
 ,
визначених співвідношеннями (3.41).
,
визначених співвідношеннями (3.41).
Припустимо,
що
– незалежна змінна (факторна ознака),
а
–
залежна змінна (результативна ознака).
Для отримання повного опису залежності
між випадковими величинами
і
потрібно знайти аналітичний вираз
сумісного розподілу цих величин, тобто
функцію:
 що, як правило, практично неможливо.
Тому під час дослідження аналітичної
залежності між випадковими величинами
і
обмежуються вивченням залежності між
однією з них і
умовним математичним сподіванням іншої,
зокрема залежністю виду:
що, як правило, практично неможливо.
Тому під час дослідження аналітичної
залежності між випадковими величинами
і
обмежуються вивченням залежності між
однією з них і
умовним математичним сподіванням іншої,
зокрема залежністю виду:
![]() –
вибіркове
рівняння регресії
на
–
вибіркове
рівняння регресії
на

![]() –
вибіркове
рівняння регресії
на
–
вибіркове
рівняння регресії
на

У
наведених вибіркових рівняннях регресії
![]() і
і
![]() –
вибіркові умовні математичні сподівання,
відповідно,
на
та
на Y,
а
–
вибіркові умовні математичні сподівання,
відповідно,
на
та
на Y,
а
 і
і
 – вибіркові функції регресії відповідно.
Аналітичні вирази
для функцій
і
будуємо на підставі проведеної вибірки
– вибіркові функції регресії відповідно.
Аналітичні вирази
для функцій
і
будуємо на підставі проведеної вибірки
 Характер відповідної регресійної моделі
допомагає вибрати діаграма розсіювання
точок
Характер відповідної регресійної моделі
допомагає вибрати діаграма розсіювання
точок
 на площині.
на площині.
Припускаючи,
що ознака
у генеральній сукупності розподілена
нормально; дисперсія результативної
ознаки
не залежить від факторної ознаки
![]() характер зв’язку між результативною
та факторною ознаками
– лінійний, тоді маємо найпростішу
регресійну модель – лінійної
регресії,
коли вибіркове
рівняння регресії
на
має такий
вигляд:
характер зв’язку між результативною
та факторною ознаками
– лінійний, тоді маємо найпростішу
регресійну модель – лінійної
регресії,
коли вибіркове
рівняння регресії
на
має такий
вигляд:

У
цьому випадку для точкових оцінок
![]() і
і
![]() можна побудувати довірчі інтервали і
оцінити їх значущість.
можна побудувати довірчі інтервали і
оцінити їх значущість.
Основним методом отримання точкових оцінок для параметрів і рівняння регресії є метод найменших квадратів.
Лінійна регресія.
Якщо дано сукупність показників y, що залежать від факторів х, то постає завдання знайти таку економетричну модель, яка б найкраще описувала існуючу залежність. Одним з методів є лінійна регресія. Лінійна регресія передбачає побудову такої прямої лінії, при якій значення показників, що лежать на ній будуть максимально наближені до фактичних, і продовжуючи цю пряму одержуємо значення прогнозу. Процес продовження прямої називається екстраполяцією. Відповідно до цього постає задача визначити цю пряму, тобто рівняння цієї прямої. В загальному вигляді рівняння прямої виглядає:
 =а+bх, (1.1)
=а+bх, (1.1)
де - вирівняне значення у для відповідного значення х.
Константи а і b - константи, які передбачають зменшення суми квадратів відхилень між фактичним значенням у і вирівняним значенням .
(у - )2 min (1.2)
Коефіцієнт а характеризує точку перетину прямої регресії з лінією координат.
Коефіцієнт b характеризує кут нахилу цієї прямої до осі абсцис, а також на яку величину зміниться при зміні х на одиницю.
Коефіцієнти а і b знаходять із системи рівнянь (1.3), що випливає з формули (1.2).
 (1.3)
(1.3)
Знайшовши значення параметрів розраховують ряд вирівняних значень для відповідних факторів і проводять дослідження знайденої економетричної моделі.
Щоб зробити висновок про доцільність використання знайденої моделі проводять аналіз за наступними напрямками:
1) Розраховують критерій Фішера та перевіряють знайдену модель на адекватність вихідним даним;
2) Розраховують і аналізують дисперсію показників;
3) Розраховують і аналізують коефіцієнт кореляції;
4) Розраховують та аналізують коефіцієнт еластичності;
5) Розраховують довірчий інтервал для прогнозованих показників.
Критерій Фішера.
Для оцінки знайденої економетричної моделі на адекватність порівнюють розрахункове значення критерію Фішера із табличним.
Розрахункове значення критерію Фішера знаходиться за формулою:
 , (1.4)
, (1.4)
де
 , (1.5)
, (1.5)
 , (1.6)
, (1.6)
n – число дослідів,
m – число включених у регресію факторів, які чинять суттєвий вплив на показник.
Для даної надійної ймовірності р (а=1-р рівня значущості) і числа ступенів вільності k1=m, k2=n-m-1 знаходиться табличне значення F(a, k1, k2). Отримане розрахункове значення порівнюється з табличним. При цьому, якщо Fроз > F(a, k1, k2), то з надійністю р = 1-а можна вважати, що розглянута економетрична модель адекватна вихідним даним. У протилежному випадку з надійністю р розглянуту лінійну регресію не можна вважати адекватною.
Дисперсія.
Дисперсія в лінійній регресії дає можливість визначити значимість характеристик, вирахуваних в регресійному аналізі (характеристики а і b). Для визначення цих характеристик використовують:
1) Загальна дисперсія - характеризує рівень відхилень між фактичними значеннями ряду і їх середнім значенням:
 (1.7)
(1.7)
2) Дисперсія, що пояснюється регресією. Чим більша доля дисперсії, що пояснюється регресією в загальній дисперсії, тим тісніший зв`язок між у і х. Чим ця доля менша, тим відповідно слабший зв`язок. Ця дисперсія визначається, як сума квадратів відхилень між вирівняним значенням ряду і середнім значенням ряду.
 . (1.8)
. (1.8)
Якщо ПД до ЗД, то зв`язок тісний між у і t.
Якщо ПД до ЗД, то зв`язок слабшає. Изображение помощника.
3) Залишкова дисперсія - це та частина ЗД, яка не пояснюється регресією
Зал.Д = ЗД – ПД,
 (1.9),
(1.9),
де уі – фактичне значення ряду.
Коефіцієнт кореляції.
Коефіцієнт кореляції r – міра тісноти зв`язку. Він на відміну від дисперсії характеризує міру тісноти зв`язку (дає її числове значення). Змінюється в межах від -1 до +1.
Якщо r=0, то лінія регресії паралельна осі абсцис, тобто залежності між у і t немає (регресія відсутня).
Якщо r +1 (додатна регресія). Із збільшенням t – уt теж буде зростати.
Якщо r -1 (від`ємна регресія). Із збільшенням t – уt буде зменшуватись.
Коефіцієнт кореляції визначається як корінь квадратний з коефіцієнта детермінації r2, що показує долю ПД в ЗД:
 , (1.10)
, (1.10)
і відповідно
 (1.11)
(1.11)
де ПД і ЗД розраховуються відповідно за формулами 1.8 і 1.7.
Знак коефіцієнта кореляції співпадає із знаком коефіцієнта b в рівнянні регресії.
Коефіцієнт еластичності.
Розрахунок коефіцієнта еластичності розраховується для кожного із факторів і показує на скільки відсотків зміниться показник, якщо фактор зміниться на 1%.
Коефіцієнт еластичності:
 (1.12)
(1.12)
Довірчий інтервал.
Вихідна економетрична модель лінійної регресії передбачає наявність випадкової величини Е, яка вимірює похибку між фактичним значенням і вирівняним значенням показника. Для розрахунку цих похибок використовують поняття "стандартного відхилення"
 , (1.13)
, (1.13)
де Sr – стандартна похибка рівняння регресії
n-2 – число значень ряду зменшене на кількість параметрів рівняння регресії (тобто а і b).
Розрахувавши стандартну похибку рівняння регресії знаходимо стандартну похибку прогнозу:
 (1.14)
(1.14)
Для
розрахунку довірчих меж потрібно знайти
значення
 .
.
Нижня
межа довірчого інтервалу
 ;
верхня межа довірчого інтервалу
;
верхня межа довірчого інтервалу
 .
.
Прогнозне значення ур=a+bxp буде знаходитись в межах від уmin до ymax.
 (1.15)
(1.15)
де t – критерій Стюдента (знаходиться з таблиць в залежності від ймовірності P і ступеня вільності n-m-1).
