1. Класичне означення імовірності. Частота та ймовірність подій.

класичне означення ймовірності – за класичним означенням імовірність випадкової події   визначається як відношення де   - кількість елементарних подій,що сприяють появі події  ;  - загальна кількість елементарних подій.

Введення класичного означення ймовірності відбулося не в результаті однократної дії, а зайняло певний проміжок часу, як і формування самої теорії ймовірностей. Тобто відбувалося безперервне вдосконалення формування, перехід від конкретних задач до загального випадку.

Найперші роботи, котрі були присвячені теорії ймовірності як науці, були написані Х. Гюйгенсом (1657) «Про розрахунки в азартних іграх». Однак у своїй праці автор не дає чіткого формулювання для класичного означення ймовірності. Це поняття було введено, хоча і в недосконалій формі, Я. Бернуллі (1713) у трактаті «Мистецтво припущень»: «Імовірність – ступінь вірогідності і відрізняється від неї, як частина від цілого». таке формулювання є досить узагальненим. Однак у п’ятій главі четвертої частини своєї роботи Я. Бернуллі описує класичну ймовірність як відношення числа «щасливих» випадків до кількості усіх можливих. Якобом Бернуллі було запропоновано й інше означення ймовірності як відношення кількості «щасливих» випадків до кількості «нещасливих». Однак в науці це означення не було прийняте з двох причин: 1) неадитивності відношень (першого та другого означень); 2) зміна відношення в останньому означенні від 0 до ∞.

Я. Бернуллі свої роботи обґрунтовував роботами Граунта і Петті. У трактаті Я. Бернуллі присутні обидві концепції теорії ймовірності – статистична і класична. Обидві вони викладені не досить чітко, однак принципово новий крок у науці було зроблено – введено в розгляд поняття ймовірності випадкової величини як числа, що знаходиться в межах від 0 до 1. Вірогідній події при цьому приписувалася 1 (максимальне значення ймовірності), а неможливій – 0 (мінімальне значення). Крім того, було ясно сказано, що це число може бути визначено двома різними способами: шляхом підрахунку кількості усіх рівноможливих випадків, які сприяють події, та всіх можливих випадків і обчислення їх відношення, а також шляхом проведення великої кількості (класичний спосіб) незалежних випробувань і обчислення частоти події (статистичний спосіб).

Саме означення, що його дав Я. Бернуллі, стало першою сходинкою у розвитку теорії ймовірності як науки. А. Муавр сприйняв це класичне означення ймовірності, яке дав Я. Бернуллі, і ймовірність події визначив точно так само, як це робимо ми. Він писав: «Ми будуємо дріб, чисельником якого буде кількість випадків появи події, а знаменником – кількість усіх випадків, при яких вона може з’явитися чи не з’явитися, такий дріб буде визначати дійсну ймовірність її появи».

З визначення імовірності випливає, що вона задовольняє співвідношення .

Приклад

З колоди 36 карт вибирається одна карта. Яка імовірність появи карти пікової масті?

Розв’язання. Нехай А ‑ поява карти пікової масті. Всього випадків 36. Число випадків, що сприяють події А, m=9. Значить Р(А)=9/36=0,25.

(Історична задача А. Муавра.) Для класичного означення А. Муавр навів приклад.

Якщо якась подія має 3 сприятливих випадки (шанси), 2 – несприятливих шанси, дробовий вираз 3/5 буде точно говорити про ймовірність її появи і може розглядатися як її міра.

Поняття ймовірності події виникло як інтуїтивне поняття, яке дає кількісну оцінку можливості появи події A i позначається Р(А).

З кожною подією A стохастичного експерименту пов'язана величина  , яку називають частотою.

Нехай ми провели експеримент n разів, і в процесі цього подія A сталася   разів. Тоді

Частота має такі властивості:

1. Невід'ємність  .

2. Адитивність 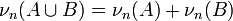 , якщо A та B - несумісні події.

3. Нормованість  .   - увесь простір елементарних подій.

Математичною моделлю частоти події є ймовірність.