10 Билет Ковариация и коэффициент корреляции.

Ковариация - это мера, учитывающая дисперсию индивидуальных значений доходности бумаги и силу связей между изменениями доходностей данной бумаги и других. Более простое определение ковариации - это мера взаимодействия двух случайных переменных.

n – число наблюдений.

Интерпретация коэффициента следующая: положительное значение ковариации говорит о том, что значения доходности этих акций изменяются в одном направлении, отрицательное значение ковариации говорит о разнонаправленных движениях между доходностями. Ковариация является низкой, если колебания доходностей двух активов в любую сторону носят случайный характер.

Ковариация двух независимых случайных величин и равна нулю.

Коэффициент корреляции лежит в интервале от -1 до +1. Значение корреляции +1 говорит о сильной взаимосвязи, т.е. активы ходят одинаково. Значение -1, наоборот, свидетельствует о разнонаправленности, т.е. рост одного из активов сопровождается падением другого. Значение 0 говорит об отсутствии корреляции.

Корреля́ция— статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин

Расчет корреляции осуществляется по формуле:

где cov(X,Y) - ковариация между X и Y. , и ,соответственно .

11 Билет Метод наименьших квадратов. Вывод формулы для построения уравнения линейной регрессии.

Метод наименьших квадратов -- один из методов регрессионного анализа для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки. Метод наименьших квадратов применяется также для приближённого представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений.

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ

Основные особенности МНК:

1) Он наиболее простой с вычислительной точки зрения.

2) Оценки коэффициентов регрессии по МНК при

определенных предпосылках обладают рядом

оптимальных свойств.

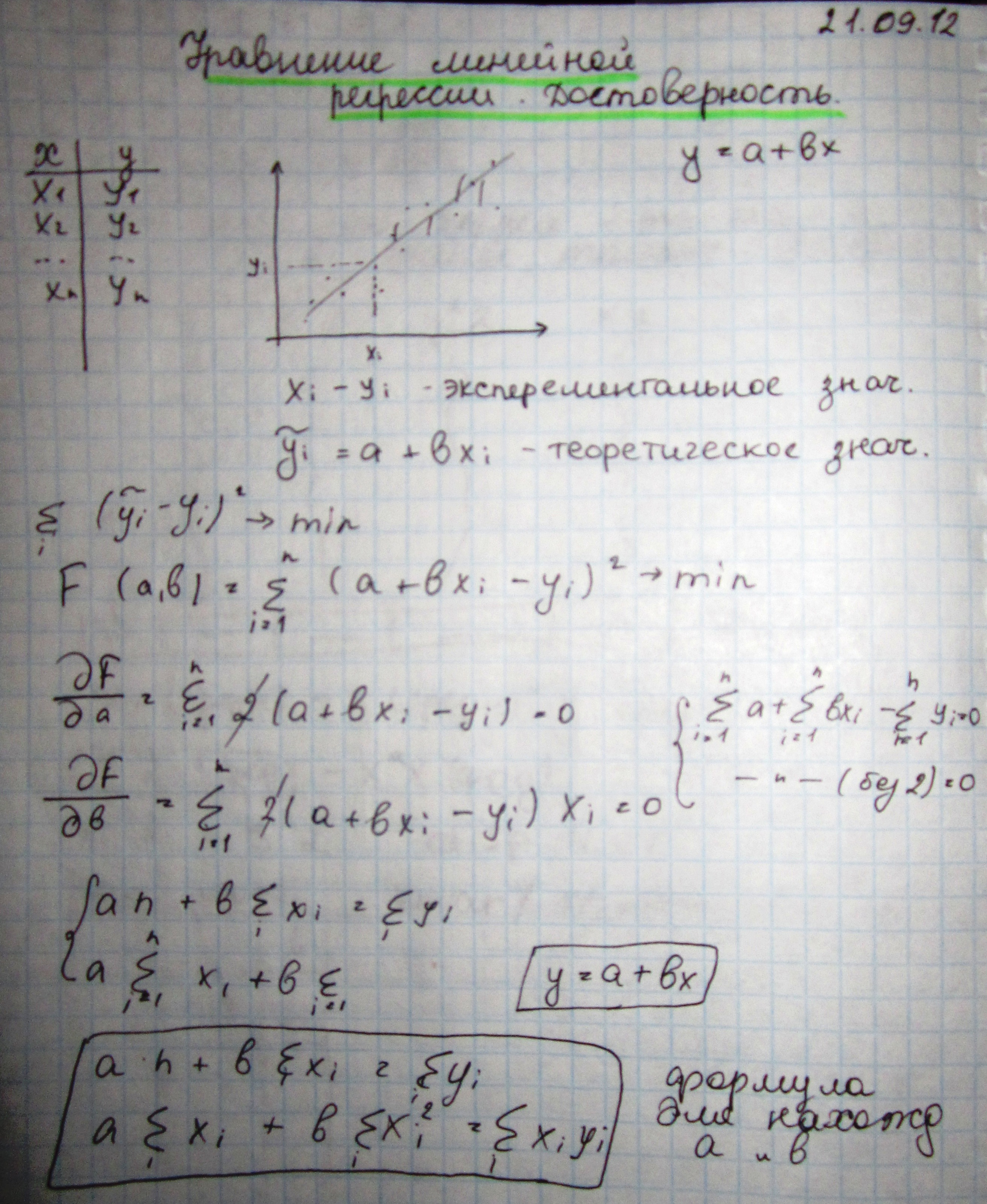
12 Билет Метод наименьших квадратов. Достоверность аппроксимации.

На практике часто приходится сталкиваться с задачей сглаживания экспериментальных данных – задача аппроксимации.

Основная задача аппроксимации – построение приближенной (аппроксимирующей) функции наиболее близко проходящей около данных точек или

около данной непрерывной функции.

Аппроксимация – процесс подбора эмпирической функции φ(х) для установления из опыта функциональной зависимости y= φ(х)

Эмпирические формулы служат для аналитического представления опытных данных.

В простейшем случае задача аппроксимации экспериментальных данных

выглядит следующим образом:

Пусть есть какие-то данные, полученные практическим путем (в ходе эксперимента или наблюдения), которые можно представить парами чисел (x,y).

Зависимость между ними отражает таблица:

xi x0 x1 x2 … xn

yi y0 y1 y2 … yn

На основе этих данных требуется подобрать функцию y=φ(x), которая наилучшим образом сглаживала бы экспериментальную зависимость между переменными и по возможности точно отражала общую тенденцию зависимости между x и y, исключая погрешности измерений и случайные отклонения. Это значит, что отклонения yi-φ(xi) в каком–то смысле были бы наименьшими.

Обычно задача аппроксимации распадается на две части:

1. Сначала устанавливают вид зависимости y=f(x) и, соответственно вид

эмпирической формулы, то есть решают, является ли она линейной, квадратичной, логарифмической или какой-либо другой.

2. После этого определяются численные значения неизвестных параметров

(констант) выбранной эмпирической формулы, для которых приближение к заданной функции оказывается наилучшим.

Возможны следующие варианты функций:

Линейная – y=ax+b. Обычно применяется в простейших случаях, когда экспериментальные данные возрастают или убывают с постоянной скоростью.

Полиномиальная – y=a0+a1x+a2 x^2 +…+an x^2^n где ai – константы. Используется для описания экспериментальных данных, попеременно возрастающих и убывающих. Степень полинома определяется количеством экстремумов (максимумов или минимумов) кривой. Полином второй степени можно описать только один максимум или минимум, полином третьей степени может иметь один или два экстремума, четвертой степени – не более трех экстремумов и т.д.

Логарифмическая – y=a·ln(x)+b, где a и b – константы, ln – функция натурального логарифма. Функция применяется для описания экспериментальных данных, которые вначале быстро растут или убывают, а затем постепенно стабилизируются.

Степенная – y=b·x^a , где a и b – константы. Аппроксимация степенной функцией используется для экспериментальных данных с постоянно увеличивающейся (или убывающей) скоростью роста. Данные не должны иметь нулевых или отрицательных значений.

Экспоненциальная – y=b·e^ax , a и b – константы, e – основание натурального логарифма. Применяется для описания экспериментальных данных, которые быстро растут или убывают, а затем постепенно стабилизируются. Часто ее использование вытекает из теоретических соображений.