1 Билет. Основные понятия комбинаторики: выборка с возвратом и без возврата, перестановки и сочетания.

Выборка с возвратом.

n^k

n – объектов

k – объем выборки (количество испытаний)

Выборка без возврата.

n(n - 1)…(n – (2 – 1))

Перестановки.

n! (1*2*3*…n) 0!=1

Сочетание.

C^kn(k-наверху, n- внизу) – количество способов выбрать k из n.

• Порядок не имеет значение

• Порядок имеет значение

Пример: кодовый замок, для открытия необходимо набрать 4 цифры. Всего 10 цифр – 0-9.

С^4 10 (4-наверху, 10 внизу)= 10*9*8*7:4*3*2*1= 210

Удобная формула: С^kn=n(n-1)…(n-k+1):k!

C^kn=n!:k!(n-k)!

2 Билет. Классическая и геометрическая вероятность.

Классическая вероятность.

Если некоторому событию А благоприятны k из n равновероятных исходов, то вероятность события: P(A)=k/n

k – благоприятные исходы

n – все события

Примеры:

К коробке 4 черных и 6 белых шаров. Извлекаем 3 шара

1. А = 2 белых и 1 черный шар

n = C³₁₀ = 10*9*8 / 1*2*3 = 120

k = C²₆ * С¹₄ = (6*5 / 1*2) * 4 = 15*4 = 60

P(A) = k/n = 60 / 120 = ½ = 0,5

2. A = 1 белый и 2 черных

k = C¹₆ * С²₄ = 6 * (4*3/1*2) = 6*6 = 36

P(A) = k/n = 36 / 120 = 6/20 = 0,3

3. А = 3 белых шара

k = C³₆ * С⁰₄ = (6*5*4 / 1*2*3) * 1 = 20*1 = 20

P(A) = k/n = 20 / 120 = 1/6

4. А = 3 черных

k = C⁰₆ * С³₄ = 1 * (4*3*2 / 1*2*3) = 1*4 = 4

P(A) = k/n = 4 / 120 = 1/30

Геометрическая вероятность

Примеры:

Бросили точку на отрезок b:

1.

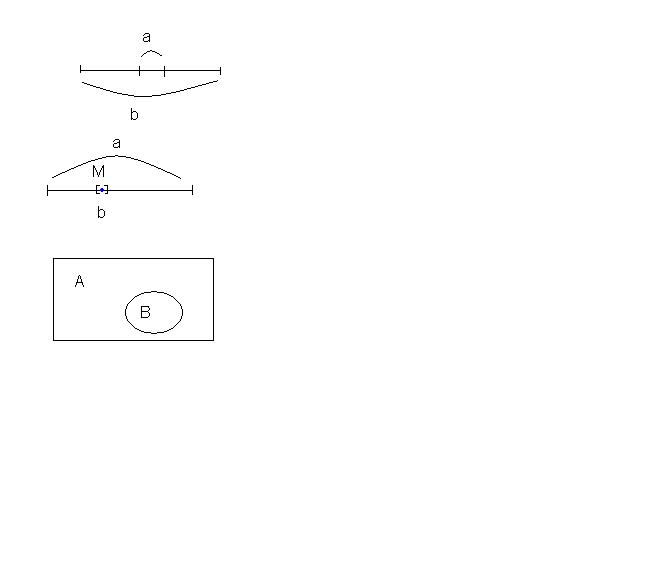P = a / b – вероятность попадания точки в отрезок а

P(M) = 0 – попадание в т.М

2.

P(B) = S(B) / S(A) – попадание в В

Геометрическая вероятность

Пусть некоторая n-мерная фигура (отрезок, плоская фигура, пространственная фигура) составляет часть другой n-мерной фигуры. Если предположить, что вероятность попадания точки на эту фигуру пропорциональна её мере (длине, площади, объёму) и не зависит от взаимного расположения меньшей и большей фигур, то вероятность попадания точки на эту фигуру определяется равенствами

где l(L), s(S), v(V) - длина, площадь и объём меньшей и большей n-мерных фигур соответственно.

Пример

На плоскости начерчены две окружности радиусами 2 и 7 см соответственно, одна внутри другой. Найти вероятность того, что точка, брошенная наудачу в большой круг, попадет также и в малый круг. Предполагается, что вероятность попадания точки в плоскую фигуру пропорциональна площади этой фигуры и не зависит от её расположения.

Решение P = s/S = πr²/πR² = 2²/7² = 4/49 ≈ 0,082

3 Билет. Алгебра событий. Вероятность суммы, произведения и дополнения событий.

Сумма событий.

Суммой двух событий А н В называют событие А + В, состоящее в появлении события А, или события В, или обоих этих событий.

Например, если из орудия произведены два выстрела и А - попадание при первом выстреле, В - попадание при втором выстреле, то А+В - попадание при первом выстреле, или при втором, или в обоих выстрелах.

В частности, если два события А и В - несовместные, то А + В - событие, состоящее в появлении одного из этих событий, безразлично какого.

Суммой нескольких событий называют событие, которое состоит в появлении хотя бы одного из этих событий.

Например, событие А + В+ С состоит из появлении одного из следующих событий: А, В, С, А и В, А и С, В и С, А и В и С.

Вероятность суммы несовместимых событий

Теорема. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

Р (A₁ + А₂ + ... + А_п) = р (A₁) + р (А₂,} + ... + р (А_п).

Следствие. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

Теорема. Сумма вероятностей событий A₁ + А₂ + ... + А_п образующих полную группу, равна единице: р (A₁) + р (А₂,} + ... + р (А_п)=1

Вероятность противоположных событий (ВИДИМО, ЭТО И ЕСТЬ ДОПОЛНЕНИЕ, НО Я НЕ ЗНАЮ!)

Противоположными называют два единственно возможных события, образующих полную группу. Если одно из двух противоположных событий обозначено через А, то другое принято обозначать А' или .Ā.

Теорема. Сумма вероятностей противоположных событий равна единице: Р(А) + Р(Ā)=1.

Замечания

1. Если вероятность одного из двух противоположных событий обозначена через р, то вероятность другого события обозначают через q. Тогда 1-p=q

2.При решении задач на отыскание вероятности события А часто выгодно сначала вычислить вероятность события А, а затем найти искомую вероятность по формуле

Р(А)=1- Р(А)

Умножения вероятностей

Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении (совмещении) этих событий.

Например. Событие А-деталь годная, Событие В-деталь окрашенная, то Событие АВ - деталь годна и окрашена.

Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий.

Например. События А, В, С-появление "герба" соответственно в первом, втором и третьем бросаниях монеты, то событие АВС - выпадение "герба" во всех трех испытаниях.