1.2.4. Решение задачи средствами MathCad
Задаём начальные значения индексов массивов:
ORIGIN:=1
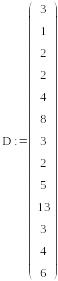
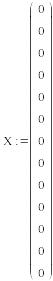Исходные
данные: вектор продолжительностей работ
D
из таблицы 1.1 и нулевые начальные значения
вектора X
дол-жны быть введены как векторы-столбцы.
Поэтому вводим их так:
или так: D:= (3 1 2 2 4 8 3 2 5 13 3 4 16)T
X:= (0 0 0 0 0 0 0 0 0 0 0 0 0)T
Ц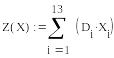
елевую
функцию Z
записываем в виде:
Вводим ограничения (знаки ≥ и = вставляются в выра-жения ограничений с помощью панели “Boolean”):
Given
Ограничения на значения X записываем в виде:
Ограничения на вершины сетевого графика Ai в соответст-вии с таблицей 1.4 представляем так:
-
X1+X2+X3+X4 =1
X10+X12+X13= 1
X1 - X5 - X6= 0
X3 - X7 - X8= 0
X2+X6 - X9= 0
X4+X8 - X10= 0
X7+X9 - X11 - X12= 0
X5+X11 - X13= 0
Для вычисления минимума или максимума целевой функ-ции используются функции соответственно Minimize и Maximize.
В качестве примера вычислим минимум целевой функции и найдём минимальную по продолжительности последователь-ность работ:
X:= Minimize(Z,X)
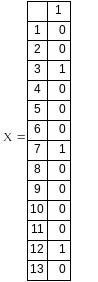Результаты
расчёта:
Z(X)=9
В результате выполнения имеем: значения элементов X3, X7, и X12 равны 1 и, следовательно, соответствующие им работы 3, 7, 12 образуют минимальную по продолжительности пос-ледовательность. Суммарная продолжительность этих работ (целевая функция Z) равна 9.
Графическая иллюстрация результатов: двойными лини-ями на сетевом графике выделяем рёбра, соответствующие работам 3, 7, 12 (рис. 1.7). Эти рёбра образуют минималь-ный по продолжительности путь в сети.
|
Рис. 1.7. Минимальный по продолжительности путь в сети. |
1.3. Состав пояснительной записки:
1. Задание.
2. Методика построения сетевого графика.
3. Рисунок сетевого графика.
4. Математическая формулировка задачи.
5. Расчётный бланк и расчётные формулы для целевой функции и левых частей ограничений.
6. Окно “Ограничения” надстройки ”Поиск решения”.
7. Результаты расчёта.
8. Графическая интерпретация результатов.