2. Скалярное произведение векторов, его свойства.

Опр. Скалярным произведением 2-х не нулевых векторов a и b называется число равное произведению длин этих векторов на cos угла между ними

Скалярное произведение 2-х векторов равно модулю одного из них умноженному на проекцию другого,на ось,сонаправленную с первым вектором

Линейные свойства скалярного произведения

1. a*b=b*a

2. 

3. a*(b+c)=a*b+a*c

4. =

5. =

9. Условия перпендикулярности и коллинеарности векторов.

Условие перпендикулярности векторов

• Векторы являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю.

• Даны два вектора a (xa;ya) и b (xb;yb). Эти векторы будут перпендикулярны, если выражение x_ax_b + y_ay_b = 0.

Условие коллинеарности векторов

• Векторы коллинеарны, если абсцисса первого вектора относится к абсциссе второго так же, как ордината первого — к ординате второго.

• Даны два вектора a (xa;ya) и b (xb;yb). Эти векторы коллинеарны, если x_a = 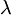x_b и y_a = y_b, где R.

10.Собственные числа и собственные векторы матрицы.

Свойства собственных чисел.

Опр. Число называется собственным числом матрицы А,если существует такой не нулевой вектор х для которого выполняется множества ах= ,вектор х называется собственным вектором соответствующим собственному числу

Теорема

Число является собственным числом матрицы А тогда и только тогда,когда выполняется равенство =0-характерестическое уравнение.Из этого уравнения находим собственные числа матрицы А.Для того чтобы найти собственный вектор,необходимо найти не нулевое решение однородной системы линейных уравнений.

Свойства собственных чисел

1)Сумма собственных чисел матрицы А=следу этой матрицы,т.е сумме её диагональных элементов

2)Произведение собственных чисел матрицы А= определителю матрицы

3)Число отличных от 0 собственных чисел матрицы А= её рангу,в частности все собственные числа матрицы А в том и только в том случае,если матрица А невырожденная

4)Если собственное число невырожденной матрицы А,то -собственное число матрицы

5)Если собственное число матрицы ,то собственное число матрицы ,при любом к 0

Теорема

Собственными числами диагональной матрицы являются числа стоящие на главное диагонали

11. Собственные числа и собственные векторы матрицы. Свойства

собственных векторов.

Свойства собственных векторов

1)Собственные векторы матрицы соответствуют различным собственным числам,линейно независимы

2)Если все собственные числа квадратной матрицы n-ого порядка различны,то соответствующие им собственные векторы образуют базис пространства

3)Любая не равная нулевому вектору линейная комбинация собственных векторов данной матрицы,соответсвующих одному и тому же числу,собственному числу этой матрицы так же является собственным вектором данной матрицы

10. Простейшие задачи аналитической геометрии (расстояние между точками,

деление отрезка в заданном отношении).

Пусть на плоскости заданы 2 точки,расстояние между ними найдём по формуле

d=