Элементы векторной алгебры и аналитической геометрии
Линейные операции над векторами (сложение, вычитание, умножение на скаляр; свойства линейных операций).
Сложение
векторов.
Пусть
и
– два произвольных вектора. Возьмем
произвольную точку О
и построим вектор
;
затем от точки А
отложим вектор
.
Вектор
,
соединяющий начало первого слагаемого
вектора с концом второго, называется
суммой
этих векторов и обозначается
(рис. 1).
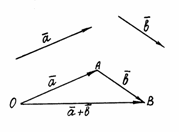
Рис. 1
Ту
же сумму можно получить иным способом.
Отложим от точки О
векторы
и
.
Построим на этих векторах как на сторонах
параллелограмм ОАСВ.
Вектор
– диагональ параллелограмма – является
суммой векторов
и
(рис. 2).
Рис. 2
Понятие суммы можно обобщить на случай любого конечного числа слагаемых (рис. 3).
Рис. 3
Вычитание
векторов. Разностью
векторов
и
называется такой вектор
,
который в сумме с вектором
дает вектор
:
.
Если векторы и привести к общему началу, то разность представляет собой отрезок, соединяющий их концы и направленный от «вычитаемого» к «уменьшаемому» (рис. 4).
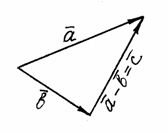
Рис. 4
Таким
образом, если на векторах
и
,
отложенных из общей точки О,
построить параллелограмм ОАСВ,
то вектор
,
совпадающий с одной диагональю, равен
сумме
,
а вектор
,
совпадающий с другой диагональю, –
разности
(рис. 5).
Рис. 5
Умножение
вектора на число. Произведением
вектора
на действительное число
называется вектор
(обозначают
),
определяемый следующими условиями:
1)
,
2)
при
и
при
.
Очевидно,
что при
.
Построим,
например, векторы
и
для заданного вектора
(рис. 6).
Рис. 6
Из определения следует: два вектора и коллинеарны тогда и только тогда, когда имеет место равенство :
(2.1)
Свойства линейных операций:
1)
;
2)
;
3)
;
;
4)
;
5)
;
6)
;
7)
;
;
Пусть
дан вектор
.
Ортом
вектора
(обозначается
)
называется вектор единичной длины,
сонаправленный с вектором
.
Очевидно,
для
любого вектора
.
Линейное (векторное) пространство.
Рассмотрим множество V элементов X,Y,Z и множество всех действительных чисел R
Пусть у нас задан закон по которому каждой паре элементов x,y ставится в соответствии элемент этого же множества v
Опр. Элемент Z называется суммой и записывается Z=x+y
Кроме
того на множестве v
задана операция умножения на число,т.е.
каждому элементу x,принадлежащему
множеству v,и
числу
ставится в соответствии число
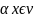
Опр. Множество V с операцией сложения и умножения на число,удовлетворяющеее указанным аксиомам,называется вещественным линейным пространством
Геометрические векторы. Определение. Основные понятия. Линейные
операции над геометрическими векторами и их свойства.
Геометрический вектор-направленный прямолинейный отрезок
Если
А-начало вектора,а В-конец,то вектор
обозначается
или
Вектор
называется
противоположным
Опр.
Длиной или
модулем вектора
называется длина отрезка АВ и обозначается
Вектор длина которого 1-называется единичным
Единичный вектор,направление которого совпадает с направлением вектора называется ортом
Опр.
Векторы
называются коллинеарными,если они лежат
на одной прямой или на параллельных
прямых
Коллинеарные векторы могут быть сонаправленными и противоположнонаправленными
Опр. Два вектора называются равными если они сонаправленные и имеют одинаковые длины
Опр. Три вектора называются коллинеарными,если они лежат в одной плоскости или в параллельных плоскостях