Линейная алгебра

1. Матрицы, типы матриц. Сложение матриц, умножение матрицы на число.

Опр.1 Прямоугольной матрицей m*n называется таблица состоящая и m-строк и n-столбцов

Виды матриц:

1)Квадратная-матрица у которой число строк равно числу столбцов

2)Строчная-матрица размера 1*n

3)Столбец-матрица размера m*1

4)Нулевая-матрица все элементы которой равны нулю

5)Единичная-матрица,элементы главной диагонали равны 1,а все остальные 0

6)Треугольник-матрица у которой все элементы ниже главной диагонали равны 0

Опр.2 Матрицы A=( ) и B=( ) называются равными если их размеры совпадают а соответсвующие элементы равны

Сумма матриц

Опр.3 Суммой матриц называется матрица C=( ),того же размера элементы которой равны суммам соответствующих элементов матриц A и B.Вычитание определяется как действие обратное сложению

Умножение матрицы на число

Опр.4 Произведением матрицы А на число £ называется матрица получающаяся из матрицы А умножением всех её элементов на число £

2. Умножение матриц. Элементарные преобразования матриц.

Умножение матрицы А на матрицу B определяется только при условии,что число столбцов матрицы А равно числу строк матрицы B.Такие матрицы называются согласованными по действию умножения

Свойства умножения

1)А*0=0

2)А*Е=Е*А=А,где Е-единичная матрица

3)(А+В)*С=А*С+В*С

4)(А*В)*С=А*(В*С)

Элементарные преобразования матриц

• перестановка местами любых двух строк матрицы;

• умножение любой строки матрицы на константу , ;

• прибавление к любой строке матрицы другой строки.

1. Определители квадратных матриц, их вычисление.

Опр.5 Определителем матрицы второго порядка называется число det A= =

2. Свойства определителей.

1)При транспонировании матрицы её определитель не меняется

2)При перестановке 2-х строк(столбцов) определитель меняет свой знак

3)Определитель имеющий 2 одинаковых столбца(строки)=0

4)Общий множитель всех элементов строки(столбца)можно вынести за знак определителя

5)Если соответствующие элементы строк(столбцов) пропорциональны,то определитель=0

6)Если каждый элемент какой либо строки(столбца) представляет собой сумму 2-х слагаемых,то определитель равен сумме 2-х определителей,у одного из которых элементами являются 1-ое слагаемое,у другого 2-ое

Все остальные строки(столбцы) у всех определителей одинаковы

7)Определитель не изменится если к элементам строки прибавить соответствующие элементы другой строки,умноженные на одно и то же число

8)Определитель равен сумме произведений элементов какой либо строки на их алгеброическое дополнение

9)Сумма произведений элементов какой либо строки на алгеброическое дополнение другой строки равны 0

3. Невырожденная матрица. Обратная матрица. Свойства обратной матрицы.

Опр.6 Квадратная матрица называется невырожденной если её определитель не равен 0

В противном случае,если определитель равен 0,то матрица А называется вырожденной

Опр.7 Матрица 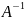называется обратной матрице А,если выполняется условие *А=А* =Е

Матрица имеет те же размеры что и матрица А

Свойства обратной матрицы

1)det ( )=

2) = *

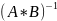3)( )^T=( )^-1