18 Билет: 1.Принципы наложения потерь энергии. Коэффициент расхода гидравлической системы. 2.Условия динамического подобия потоков жидкости и газов. Число Фруда.

Динамическое подобие означает пропорциональность сил, действующих на сходственные элементы кинематически подоб­ных потоков и равенство углов, характеризующих направление этих сил.

В потоках жидкостей обычно действуют разные силы — давле­ния, вязкости (трения), тяжести и др. Соблюдение пропорциональ­ности всех этих разнородных сил означает так называемое полное гидродинамическое подобие.

Условие динамического подобия по­токов:

или, переходя к обратным величинам,

В случаях безнапорных течений под действием разности нивелирных высот вопрос о подобии осложняется, так как приходится вводить еще один критерий подобия — число Фруда, учиты­вающее влияние на движение жидкости силы тяжести. Однако для подавляющего большинства интересующих нас задач в области авиационной техники этот критерий не имеет значения, и мы его рассматривать не будем.

Итак, в подобных потоках, мы имеем равенство безразмерных коэффициентов и чисел , , , Eu, Ne, Re и некоторых других, которые будут введены и рассмотрены ниже. Изменение числа Re означает, что меняется соотношение основных сил в потоке, в связи с чем указанные коэффициенты могут также меняться. Поэтому все эти коэффициенты в общем случае следует рассматривать как функции числа Re (хотя в некоторых интервалах числа Re они могут оставаться постоянными).

19 Билет: 1.Вывод уравнения Бернулли для несжимаемой жидкости.

Будем рассматривать установившееся течение идеальной жид­кости, находящейся под воздействием лишь одной массовой силы — силы тяжести, и выведем для этого случая основное уравнение, связывающее между собой давление в жидкости и скорость ее дви­жения.

Возьмем одну из струек, составляющих поток, и выделим сече­ниями 1 и 2 участок этой струйки произвольной длины (рис. 24). Пусть площадь первого сечения равна dS₁, скорость в нем V₁, дав­ление р₁, а высота расположения центра тяжести сечения, отсчи­танная от произвольной горизонтальной плоскости Z₁. Во втором сечении аналогично.

За бесконечно малый отрезок времени dt выделенный нами уча­сток струйки под воздействием внешних сил переместится в поло­жение 1’—2'.

Применим к этому участку струйки теорему механики о том, что работа сил, приложенных к телу, равна приращению кинети­ч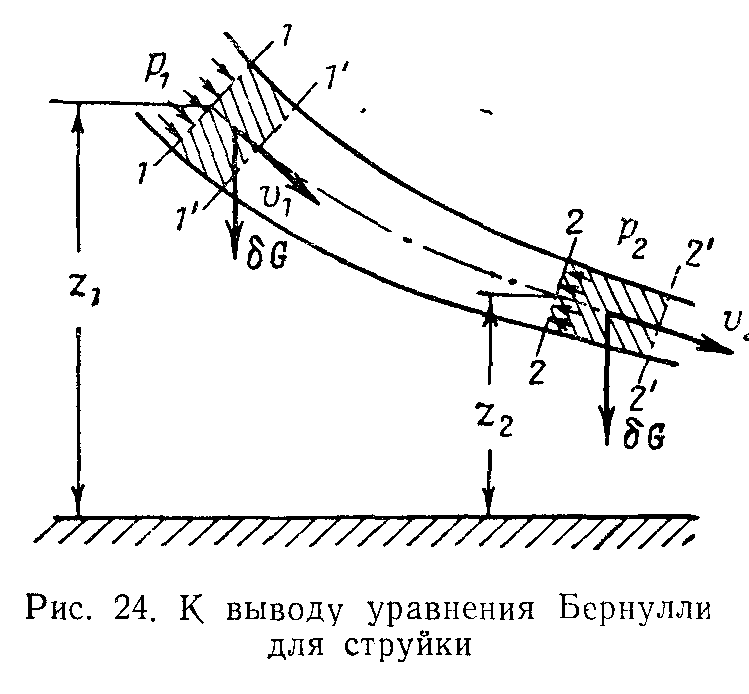 еской энергии этого тела. Такими силами в данном слу­чае являются силы давления, действующие нормально к по­верхности рассматриваемого участка струйки, и лишь одна из массовых сил — сила тяжести.

Подсчитаем работу сил дав­ления, силы тяжести и измене­ние кинетической энергии уча­стка струйки за сремя dt.

Работа силы давления в первом сечении будет поло­жительна, так как направле­ние силы совпадает с направ­лением перемещения, и выразится как произведение силы (p₁dS₁) на путь (V₁dt}, т. е.

Работа силы давления во втором сечении будет иметь знак ми­нус, так как направление силы прямо противоположно направле­нию перемещения, и определится выражением

Силы давления, действующие по боковой поверхности отрезка струйки, работы не произведут ввиду того, что они нормальны к этой поверхности, а следовательно, нормальны и к перемеще­ниям.

Итак, работа сил давления будет равна

Работа силы тяжести равна изменению потенциальной энергии положения участка струйки. Веса отрезков 1—1’ и 2—2' равны меж­ду собой, т. е.

Поэтому работа силы тяжести выразится

Приращение кинетической энергии будет равно

Сложив работу сил давления с работой силы тяжести и приравняв эту сумму к приращению кинетической энергии, получим

Разделим все члены уравнения на вес. После соответствую­щих сокращений получим

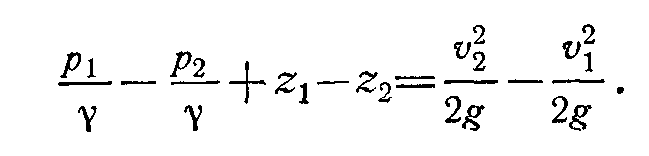
Сгруппируем члены, относящиеся к первому сечению, в левой части уравнения, а относящиеся ко второму сечению—в правой части уравнения:

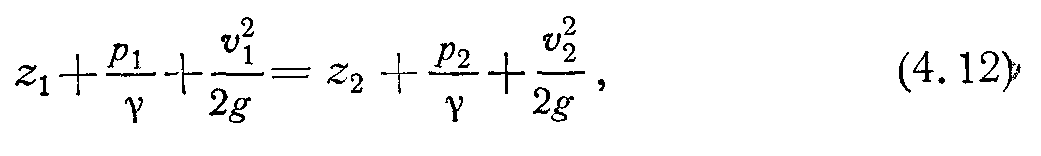
где соответствующие составляющие - нивелирная высота или геометрический напор; пьезометрическая высота или пьезометрический напор; скоростная высота или скоростной напор.

Полученное уравнение называется уравнением Бернулли для струйки идеальной несжимаемой жидкости.

Трехчлен вида

называется полным напором.

Уравнение Бернулли (4.12) записано для двух произвольно взятых сечений струйки, первого и второго, и выражает равенство полных напоров Н в этих сечениях. Так как эти сечения взяты со­вершенно произвольно, то, следовательно, и для любого другого сечения этой же струйки полный напор будет иметь то же значе­ние, т. е.

Итак,для идеальной движущейся жидкости сум­ма трех высот: нивелирной, пьезометрической и скоростной есть величина, постоянная вдоль струйки.

Из уравнения Бернулли и уравнения расхода следует, что, если площадь поперечного сечения струйки уменьшается, т. е. струйка сужается, то скорость течения жидкости увеличивается, а давление уменьшается, и наоборот, если струйка расширяет­ся, то скорость уменьшается, а давление возрастает.

Рассмотрим физический или, точнее, энергетический смысл уравнения Бернулли. Условимся называть удельной энергией жид­кости энергию, отнесенную к единице веса, т. е.

Удельная энергия имеет линейную размерность, так же как и члены уравнения Бернулли. Нетрудно показать, что члены урав­нения Бернулли являются различными формами удельной механи­ческой энергии жидкости, а именно:

z —удельная энергия положения,

p/ —удельная энергия давления движущейся жидкости,

z+ p/ — Удельная потенциальная энергия жидкости;

²/2g – Удельная кинетическая энергия жидкости;

Н – полная удельная энергия движущейся жидкости.

Таким образом, энергетический смысл уравнения Бернулли для элементарной струйки идеальной жидкости заключается в постоян­стве вдоль струйки полной удельной энергии жидкости. Уравнение Бернул­ли, следовательно, выражает собой за­кон сохранения механической энергии в идеальной жидкости.

В процессе движения идеальной жидкости одна форма энергии может превращаться в другую форму, но полная удельная энер­гия при этом, как следует из уравнения Бернулли, остается без изменения.

Уравнение Бернулли для струйки идеальной жидкости может быть также легко получено путем интегрирования дифференци­альных уравнений движения идеальной жидкости.