2.Условия динамического подобия потоков жидкости и газов. Число Маха. 14 билет: 1.Примеры на практическое применение уравнения Бернулли.

Полученное в предыдущих параграфах уравнение Бернулли яв­ляется основным законом установившегося движения жидкости.

Рассмотрим ряд устройств, действие которых основано на применении данного закона.

Дроссельный расходомер (расходомер Вентури).

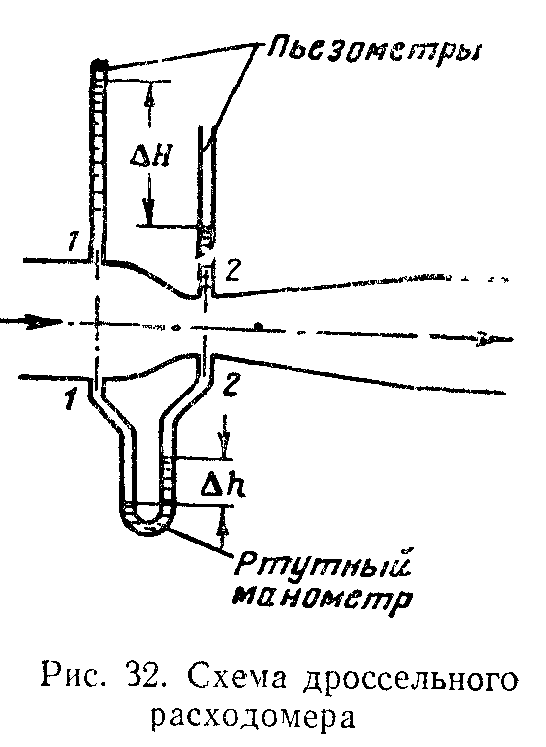
Запишем для первого и второго сечений потока уравнение Бернулли и уравнение расхода (считая распределение скоростей рав­номерным) :

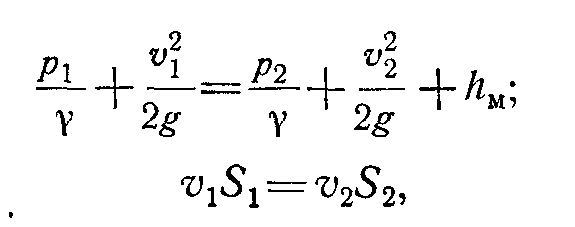
где h_м — потеря напора между сечениями /—/ и 2—2. Учитывая, что

Найдем из этой системы уравнений одну из скоростей:

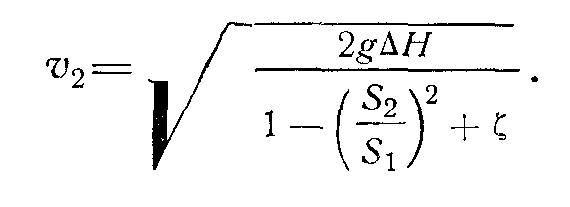
Отсюда объемный расход равен

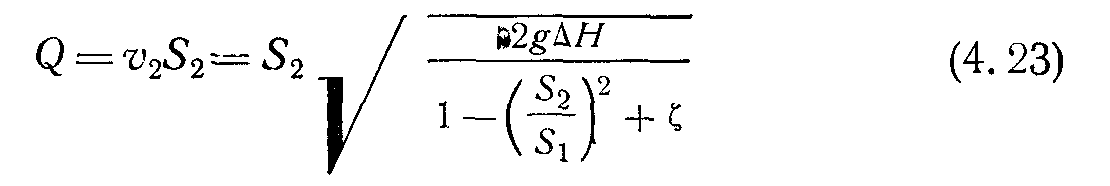
или

где С—величина постоянная для данного расходомера,

Кроме того, расходомер можно выполнить в виде диафрагм, мерных сопел.

Трубка полного напора (или трубка Пито) может быть исполь­зована для измерения скорости потока. Пусть жидкость движется в открытом русле со скоростью  (рис. 36). Если установить в этом потоке трубку, изогнутую под прямым углом, отверстием А на­встречу потоку, то жидкость в этой трубке поднимется над свобод­ной поверхностью на высоту, равную скоростной высоте. Объясня­ется это тем, что скорость частиц жидкости, попадающих в отвер­стие трубки, уменьшается до нуля, а давление, следовательно, уве­личивается на величину скоростного напора. Измерив высоту подъ­ема жидкости в трубке, легко определить скорость потока.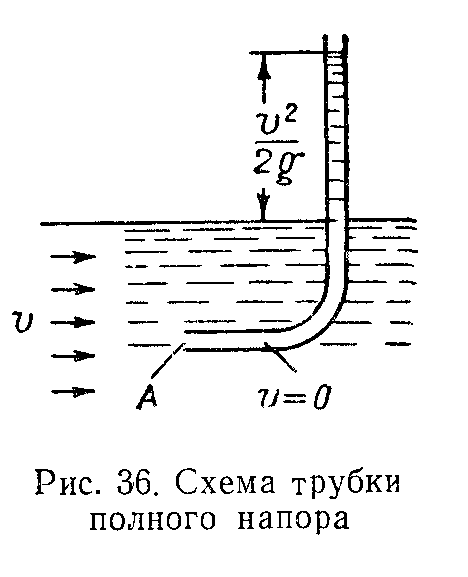

На этом же принципе основано измерение скорости полета са­молета. На рис. 37 показана схема самолетной скоростной трубки (насадка) для малых скоростей полета (по сравнению со ско­ростью звука).

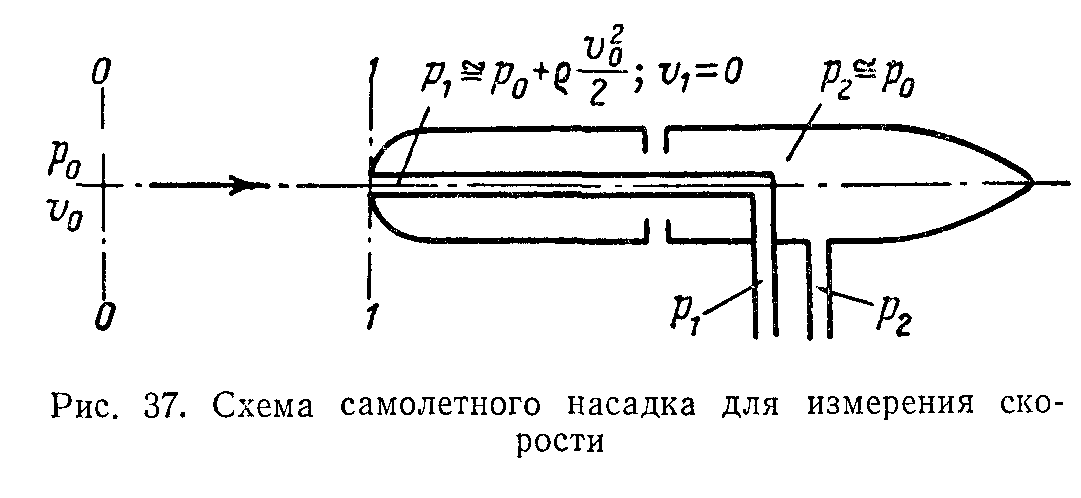
Запишем уравнение Бернулли для элементарной струйки, кото­рая набегает на трубку вдоль ее оси, а затем растекается по ее по­верхности. Взяв сечения 0—0 (невозмущенный поток) и 1—1(где =0), будем иметь

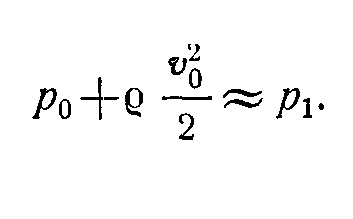
Так как боковые отверстия трубки приближенно воспринимают давление невозмущенного потока, то р₂р_о, следовательно, из пре­дыдущего имеем

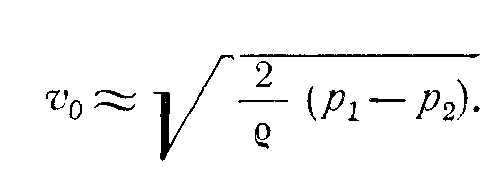
2.Теоретический и действительный расход жидкости. Коэффициент расхода. 15 билет: 1.Приборы для определения скорости и расхода жидкости. 2.Условия динамического подобия потоков жидкости и газов. Число Рейнольдса.

Динамическое подобие означает пропорциональность сил, действующих на сходственные элементы кинематически подоб­ных потоков и равенство углов, характеризующих направление этих сил.

В потоках жидкостей обычно действуют разные силы — давле­ния, вязкости (трения), тяжести и др. Соблюдение пропорциональ­ности всех этих разнородных сил означает так называемое полное гидродинамическое подобие.

Условие динамического подобия по­токов:

или, переходя к обратным величинам,

закон подобия Рейнольдса, который можно сформулировать следующим образом: для гидродинамиче­ского подобия геометрически подобных потоков с учетом сил вязкости требуется равенство чи­сел Рейнольдса, подсчитанных для любой пары сходственных сечений этих потоков.

Число Re есть величина, пропорциональная отношению динамиче­ского давления к напряжению трения или, что то же самое, от­ношению сил инерции к силам вязкости. Чем больше скорость и поперечные размеры потока и чем меньше вязкость жидкости, тем больше число Re. Для потока идеальной жидкости число Re бесконечно велико, так как вязкость =0. 16 билет: 1.Уравнение энергии для потока вязкой жидкости. 2.Способы экспериментального осуществления условий динамического подобия потоков. 17 билет: 1.Принципы наложения потерь энергии. Коэффициент расхода гидравлической системы. 2.Ламинарное и турбулентное течение вязкой жидкости и газа.

Ламинарное течение — это слоистое течение без перемешива­ния частиц жидкости и без пульсаций скорости. При таком течении все линии тока вполне определяются формой русла, по которому течет жидкость. При ламинарном течении жидкости в прямой трубе постоянного сечения все линии тока направлены параллель­но оси трубы, т. е. прямолинейны; отсутствуют поперечные пере­мещения частиц жидкости, а потому не происходит перемешивания жидкости в процессе ее течения Пьезометр, присоединенный к трубе с установившимся ламинарным течением, показывает неизмен­ность давления (и скорости) по времени, отсутствие колебаний (пульсаций). Таким образом, ламинарное течение является вполне упорядоченным и при постоянном напоре строго установившимся течением (хотя в общем случае может быть и неустановившимся)

Однако ламинарное течение нельзя считать безвихревым, так как в нем хотя и нет ярко выраженных вихрей, но одновременно с поступательным движением имеет место упорядоченное враща­тельное движение отдельных частиц жидкости вокруг своих мгно­венных центров с вполне определенными угловыми скоростями.

Турбулентное течение — это течение, сопровождающееся интенсивным перемешиванием жидкости и пульсациями скоростей и давлений. При турбулентном течении линии тока лишь примерно определяются формой русла. Движение отдельных частиц оказы­вается неупорядоченным, траектории подчас имеют вид замысловатых кривых. Объясняется это тем, что при турбулентном течении наряду с основным продольным перемещением жидкости вдоль русла имеют место поперечные перемещения и вращательное дви­жение отдельных объемов жидкости.

Смена режима течения данной жидкости в трубе происходит при определенной скорости течения, которую называют критиче­ской. Как показывают опыты, значение этой скорости прямо пропорционально кинематическому коэффициенту вязкости и обратно пропорционально диаметру трубы, т. е.

Оказывается, что входящий сюда безразмерный коэффициент пропорциональности k имеет универсальное значение, т. е. одинаков для всех жидкостей и газов и любых диаметров труб. Это означает, что смена режима течения происходит при впол­не определенном соотношении между скоростью, диаметром и вяз­костью, равном

Это безразмерное число называется критическим числом Pейнольдса по имени английского ученого, который установил этот критерий, и обозначается

Как показывают опыты, критическое число Рейнольдса прибли­зительно равно 2300.

Однако можно говорить не только о критическом числе Re_кр, соответствующем смене режима, но и о фактическом числе Рей­нольдса для того или иного потока и выражать его через факти­ческую скорость, т. е.

Таким образом, мы получаем критерий, позволяющий судить о режиме течения жидкости в трубе. При значениях числа Rе<Rе_кр течение оказывается ламинарным; при Rе>Rе_кр течение обычно турбулентное.

Зная скорость течения жидкости, диаметр трубы и вязкость жидкости, можно расчетным путем определить режим течения жид­кости, что очень важно для последующих гидравлических расчетов.

Ламинарные течения на практике встречаются в тех случаях, когда по трубам движутся весьма вязкие жидкости, например, сма­зочные масла, глицериновые смеси и др.

Турбулентное течение обычно имеет место в водопроводах, а также в трубах, по которым движутся бензин, керосин, спирты и кислоты. Таким образом, на самолете приходится сталкиваться как с ламинарным, так и с турбулентным режимами течения жид­костей в трубах; в самолетных маслосистемах и гидропередачах режим течения чаще всего ламинарный, а в топливных системах — турбулентный.

Смена режимов течения при достижении числа Rе_кр объясняет­ся тем, что один режим течения теряет устойчивость, а другой ее приобретает. При Re<Re_кp ламинарный режим является вполне устойчивым; всякого рода искусственная турбулизация потока и его возмущения (сотрясения трубы, введение в поток колеблю­щегося тела и пр.) погашаются влиянием вязкости и ламинарный поток восстанавливается. Турбулентный режим при этом не­устойчив.

При Re>Re_кp, наоборот, турбулентный режим устойчив, а лами­нарный — неустойчив.

В связи с этим критическое число Re_кp, соответствующее пере­ходу от ламинарного режима к турбулентному, может получиться несколько больше, чем Re_кp для обратного перехода. В особых ла­бораторных условиях при полном отсутствии факторов, способст­вующих турбулизации потока, удается получить ламинарный ре­жим при числах Re, значительно больших Re_кp. Однако в этих случаях ламинарное течение оказывается настолько неустойчивым, что достаточно, например, небольшого толчка, чтобы ламинарный поток быстро превратился в турбулентный. На практике, особенно в самолетных трубопроводах, мы обычно имеем условия, способ­ствующие турбулизации, — вибрация труб, местные гидравлические сопротивления, неравномерность (пульсации) расхода и пр., а по­тому указанное обстоятельство имеет в гидравлике скорее прин­ципиальное значение, чем практическое.

Точнее говоря, вполне развитое турбулентное течение в трубах устанавли­вается при Re> Re’_кp=4000, а при Re=2300—4000 имеет место переходная, кри­тическая область.

Вопрос об устойчивости ламинарного режима течения и о ме­ханизме турбулизации теоретически пока еще полностью не решен. Но исследования показывают, что в данном сечении цилиндрической трубы турбулизации способствуют такие факторы, как рас­стояние от стенки, величина скорости и ее поперечного градиента d/dy. Наибольшее расстояние от стенки и наибольшая скорость имеют место в центре потока, но там равен нулю градиент. У стенки, наоборот, градиент скорости наибольший, а скорость и расстояние у наименьшие или даже равны нулю. Поэтому на­чальная турбулизация ламинарного потока в прямой трубе посто­янного сечения начинается где-то в промежутке между осью трубы и стенкой, но все же ближе к стенке.

В трубах переменного сечения турбулизация потока происхо­дит не так, как в цилиндрической трубе. В расширяющихся тру­бах наблюдается замедление течения, усиливается тенденция к поперечному перемешиванию и значение Re_кp уменьшается. В су­жающихся трубах происходит ускорение течения и выравнивание скоростей по сечению, тенденция к перемешиванию уменьшается, а значение Re_кp увеличивается.