4.Классы элементарных функций. Основные элементарные функции.

Функция у = у(х) называется элементарной, если её можно задать одним аналитическим выражением, так что каждое значение у получается из х при помощи конечного числа элементарных операций .

Основными элементарными функциями называются следующие:

1. Целая рациональная функция или (многочлен): y=a₀xⁿ+a₁x^n-1+...+a_n, где n - целое неотрицательное число (степень многочлена), a₀, a₁, ..., a_n - постоянные числа (коэффициенты).

2. Дробно-рациональная функция, которая является отношением двух целых рациональных функций.

3. Иррациональная функция - это та, которая строится с помощью суперпозиции рациональной функции и степенных функций с рациональными показателями. Пр.: у=ах^p/q, где p, q прин. Z.

Рациональная и иррациональная функции образуют класс алгебраических функций.

Следующие функции образуют класс трансендентных функций.

4.Показательная функция у = а^х, где а > 0, а ≠ 1.

5.Логарифмическая функция у = log_ax, где а > 0, а ≠ 1.

6. Тригонометрические функции y = sin x, y = cos x, y = tg x, y = ctg x

7. Обратные тригонометрические функции y = arcsin x, y = arccos x,

y = arctg x, y = arcctg x.

8. Гиперболи́ческие фу́нкции sh(x), ch(x), th(x).

Рассмотрим подробнее основные элементарные функции и их графики.

Показательная функция (рис. 1.6).

; .

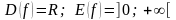При функция строго убывает, при 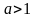строго возрастает.

Логарифмическая функция.

Л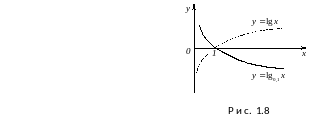 огарифм с основанием 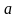(рис. 1.8).

, .

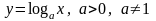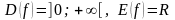При функция строго убывает,

при строго возрастает.

5.Бесконечно малые и бесконечно большие величины и функции.

Бесконечно малые.

Переменная х называется бесконечно малой, если для любого сколь угодно малого наперед заданного   , существует такой момент в измерении х , начиная с которого переменная величина х по модулю становится и остаётся меньше   .

Если  х - бесконечно малая то говорят, что  х стремится к нулю, и пишут: х   .

Бесконечно большие.

Переменная x называется бесконечно большой, если для всякого наперёд заданного сколь угодно большого положительного числа с существует такой момент в её измерении, начиная с которого эта величина по модулю становится и остаётся больше с. Пишут: с 

Величина, обратная  бесконечно большой, есть величина бесконечно малая, и обратно. 

О п р е д е л е н и е 1. Функция y = f (x) называется бесконечно малой (Б.М.В.) при или , если ее предел равен нулю

                                

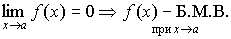
О п р е д е л е н и е 2. Функция y = f (x)  называется бесконечно большой при или , если её предел при элих условиях равен бесконечности.

   или    .                     

Для б.б. и б.м. фун-й справедливы все теоремы и св-ва, характ-ые для б.б. и б.м. величин.

6. Свойства бесконечно малых величин

1. Алгебраическая сумма (разность) бесконечно малых величин есть величина бесконечно малая.

2. Произведение бесконечно малой величины на ограниченную величину есть величина бесконечно малая.

Следствия:

1. Произведение бесконечно малой величины на константу С или на функцию, имеющую конечный предел 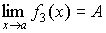, есть величина бесконечно малая.

2. б.м.в. в положительной степени есть б.м.в.