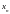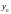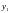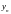- •Числа, множества и операции над ними.
- •Функция. Основные определения и понятия .Способы её задания.
- •3.Взаимообратные и сложные функции. Сложная функция.
- •Обратная функция.
- •4.Классы элементарных функций. Основные элементарные функции.
- •5.Бесконечно малые и бесконечно большие величины и функции.
- •6. Свойства бесконечно малых величин
- •7. Свойства б.Б.В.
- •3. Произведение бесконечно большых величин есть величина бесконечно большая.
- •8. Сравнение бесконечно малых функций. Эквивалентные бесконечно малые функции.
- •Определения
- •Эквивалентные величины
- •9. Бесконечные числовые последовательности. Предел последовательности.
- •Предел последовательности
- •10. Предел функции.
- •11. Теоремы о пределах.
- •12. Односторонние пределы.
- •13. Предел функции в бесконечности
- •14. Свойства непрерывных функций
- •15. Предел рациональной и дробно - рациональной функций.
- •16. Первый и второй замечательные пределы
- •17. Непрерывность функции в точке, на интервале и на отрезке.
- •18. Разрывы функций первого и второго рода. Устранимые разрывы.
- •19. Задача о мгновенной скорости движения. Механический смысл производной.
- •Механический смысл первой производной.
- •Механический смысл второй производной.
- •20. Математическое определение и геометрический смысл производной.
- •Составим отношение
- •Геометрический смысл производной
- •21. Непрерывность и дифференцируемость функций
- •22. Основные Правила дифференцирования
- •23. Производная обратной и сложной функций.
- •Доказательство. Итак
- •30. Дифференцирование неявных функций
- •31.Дифференцирование функций заданных параметрически и в полярной
- •32.Понятие о дифференциале функции и его геометрический смысл.
- •33. Производные высших порядков.
- •34.Дифференциалы высших порядков. Формула Лейбница .
- •Формула Лейбница
- •35. Теоремы Ферма, Ролля, Лагранжа и Коши. Их геометрический смысл.
- •38.Возрастание и убывание функций. Понятие об экстремуме.
- •39.Признак возрастания и убывания функции.
- •Доказательство. 1-я часть. Пусть f(X) на [a,b]. Придадим X приращение X и рассмотрим
- •40.Необходимое и достаточное условие существования экстремума.
- •41.Схема исследования функции на экстремум.
- •42. Исследование функции на экстремум с помощью второй производной.
- •Наибольшее и наименьшее значения функции на отрезке.
- •43.Формулы Тейлора и Маклорена Формула Тейлора
- •45.Исследование функций на экстремум с помощью формулы Тейлора
- •46.Выпуклость и вогнутость графика функции. Точки перегиба. Необходимое и
- •47.Асимптоты функции.
- •Горизонтальные асимптоты.
- •48.Исследование кривых, заданных параметрически (астроида, циклоида)
- •Пусть , исследуем аналогично .
- •Исследование функций, заданных в полярных координатах , можно исследовать как и параметрические, если перевести в декартовую систему координат.
- •49.0Бший план исследования функции и построения ее графика.
- •50.Касательная и нормаль к плоской кривой.
- •51.Приближенное решение уравнений. Метод Ньютона (касательных) Действительные корни .
- •52.Приближенное решение уравнений. Методы хорд, итераций и
- •54. Векторная функция скалярного аргумента и ее дифференцирование.
- •55.Свойства производной от векторной функции по скалярному аргументу.
- •56,Кривизна пространственной кривой. Сопровождающий трехгранник
- •57.Уравнения касательной, нормали, бинормали и плоскостей
- •51.Приближенное решение уравнений. Метод Ньютона (касательных) Действительные корни .
- •52.Приближенное решение уравнений. Методы хорд, итераций и
- •60.61.Интерполяция. Интерполяционный многочлен Лагранжа. Конечные разности и интерполяционная формула Ньютона
- •Интерполирующая функция Лагранжа.
60.61.Интерполяция. Интерполяционный многочлен Лагранжа. Конечные разности и интерполяционная формула Ньютона
Пусть
из результатов нам известны числовые
значения
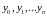 некоторой функции
некоторой функции
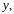 соответствующие числовым значениям
соответствующие числовым значениям
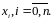 Можно считать, что
Можно считать, что
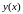 задана таблично:
задана таблично:
Довольно
часто возникает потребность в вычислении
промежуточных значений
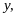 не имеющихся в таблице. Часто решается
задача поиска аналитического вида
функции, заданной таблично. При этом
ищется такая функция, чтобы при
не имеющихся в таблице. Часто решается
задача поиска аналитического вида
функции, заданной таблично. При этом
ищется такая функция, чтобы при
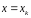 она принимала значения
она принимала значения
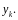
Решение этих задач составляет раздел вычислительной математики, называемый интерполированием функций.
Интерполяция - Оценка значения неизвестной величины, находящейся между двумя точками ряда известных величин.
Интерполирующая функция Лагранжа.
Пусть
мы имеем таблично заданную функцию.
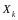 называют узлами интерполяции. И пусть
называют узлами интерполяции. И пусть
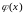 есть интерполирующий многочлен вида:
есть интерполирующий многочлен вида:
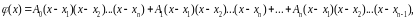
где
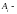 константы,
подлежащие определению. Для их нахождения
поочерёдно будем полагать
константы,
подлежащие определению. Для их нахождения
поочерёдно будем полагать
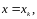 требуя при этом, чтобы
требуя при этом, чтобы
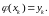 Мы получим
Мы получим
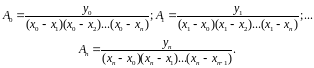
Подставляя
найденные значения
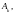 получим интерполяционную формулу
Лагранжа:
получим интерполяционную формулу
Лагранжа:
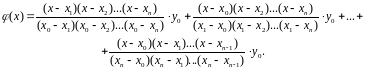
Полагая
в этой формуле
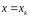 мы всегда имеем
мы всегда имеем
 и получим возможность оценки значений
соответствующих значениям
и получим возможность оценки значений
соответствующих значениям
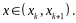
Найденное
выражение
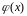 позволяет выполнить и оценку производной
позволяет выполнить и оценку производной
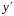 в некоторых точках.
в некоторых точках.
Интерполяционная формула Ньютона.
Если узлы интерполяции являются равноотстоящими, т.е. образуют арифметическую прогрессию:
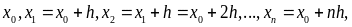
где
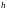 называют шагом интерполяции, то лучше
использовать более простую интерполяционную
формулу Ньютона. Эта формула построена
на т.н. конечных разностях функции
называют шагом интерполяции, то лучше
использовать более простую интерполяционную
формулу Ньютона. Эта формула построена
на т.н. конечных разностях функции
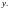
Определение. Конечной разностью первого порядка величины называют разность между двумя её последовательными табличными значениями.
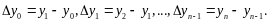
Конечной разностью второго порядка называется разность между двумя последовательными разностями первого порядка
Аналогично определяются разности более высоких порядков.
Для
вывода формулы Ньютона нам потребуются
конечные разности до порядка
 включительно. Поэтому составляется
таблица:
включительно. Поэтому составляется
таблица:

Используя эту таблицу можно найти
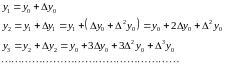
(*) 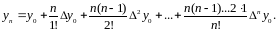
В
(*)
есть
табличный номер
или число шагов, отделяющих табличное
значение
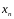 от
от
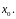 Т.е.
Т.е.
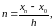 т.к.
т.к.
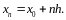
Если
теперь вычислять нетабличное
и сохранить вид правой части (*), то
величина
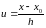 будет давать нам
для любого табличного
будет давать нам
для любого табличного
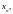 тогда как для
тогда как для
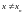 мы будем получать значения
мы будем получать значения
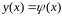 т.е.
т.е.
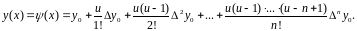
В
развернутой форме
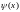 является многочленом степени не выше
и представляет собой интерполяционную
формулу
Ньютона.
является многочленом степени не выше
и представляет собой интерполяционную
формулу
Ньютона.
Можно показать, что для равноотстоящих узлов формулы Лагранжа и Ньютона дают один и тот же многочлен, т.е. являются тождественными.