1. Числа, множества и операции над ними.

Одним из основных понятий математики является число. Положительные числа 1,2,3, … , которые получаются при счете, называются натуральными. Числа … -3,-2,-1,0,1,2,3,… называют целыми. Числа, которые могут быть представлены в виде конечного отношения двух целых чисел 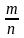( 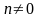) называются рациональными. К ним относятся целые и дробные, положительные и отрицательные числа. Числа, которые представляются бесконечными непериодическими дробями называются иррациональными. Примерами иррациональных чисел служат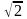 , . В множестве иррациональных чисел выделяют трансцендентные числа. Это числа, которые являются результатом неалгебраических действий. Наиболее известными из них являются число 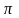и число . Числа рациональные и иррациональные называются действительными. Действительные числа изображаются точками на числовой оси.

Числовой осью называется прямая, на которой указана точка начала отсчёта, направление возрастания и единица масштаба.

Между двумя точками числовой оси всегда найдутся как рациональные так и иррациональные точки.

Теорема: любое иррациональное число «альфа» всегда можно представить с любой степенью точности рациональным числом.

Определение: абсолютной величиной или модулем числа х (|х|) называется неотрицательное число, которое равняется самому числу х, если х>=0 и –х, если х<0.

Множество - это совокупность, набор элементов, объединенных общими свойствами.

Объект, принадлежащий множеству, называется его элементом.

Множества обозначаются заглавными латинскими буквами А, В, С… , а элементы множества строчными латинскими буквами a, b, c… .

Основное отношение между элементами и множеством - это отношение принадлежности элемента множеству. Оно обозначается знаком     означает, что элемент x принадлежит множеству A.    означает, что элемент x не входит в множество А.   означает, что каждый элемент множества A является также элементом множества B. В этом случае множество A называется подмножеством множества B. Если   и   то A=B, т.е. множества A и B равны. Если   и   то A называется собственным подмножеством множества B, и в этом случае пишем   Множество, не содержащее элементов, называется пустым и обозначается   .

Способы задания множеств:

1. Если множество конечно, то его можно задать перечислением  всех его элементов. 

2. Множество можно задать указанием характеристического свойства его элементов.

Основные операции:

1.   Объединением множеств A и B называется множество элементов, принадлежащих по крайней мере одному из данных множеств (т. е. либо A, либо B, либо одновременно и A и B). Обозначают   и читают "объединение A и B".

   2.  Пересечением множеств A и B называется множество элементов, принадлежащих одновременно и A и B. Обозначают   и читают "пересечение A и B".

Если множества не имеют общих элементов, то пересечение пустое.

  3.   Разностью множеств A и B называется множество элементов, принадлежащих A и не принадлежащих B. Обозначают A\B и читают "разность Aи B".

4. Операция дополнения подразумевает некоторый универсум (универсальное множество  , которое содержит  ):

Относительным же дополнением называется А\В