33 Структурные схемы передатчиков связи с угловой модуляцией.
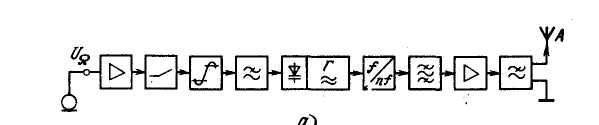
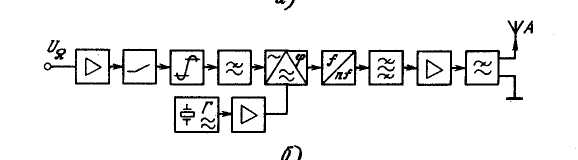
Первая схема использует прямую ЧМ варикапом в кварцевом АГ. Модулирующий сигнал усиливается и подвергается частотной предкоррекции, ограничению амплитуды (или сжатию динамического диапазона). ФНЧ ограничивает спектр модулирующего сигнала. В кварцевом АГ осуществляется прямая ЧМ, затем умножение частоты для увеличения глубины модуляции и перехода в рабочий диапазон. Полосовой фильтр ослабляет субгармоники. ГВВ обеспечивает необходимый уровень мощности передатчика, ФНЧ — ослабление высших гармоник до допустимого уровня (около - 40...60 дБ) и согласование с антенной.
В передатчике с косвенным методом получения ЧМ, в фазовом модуляторе осуществляется ФМ несущего колебания, спектр модулирующего сигнала перед входом модулятора может подвергаться дополнительной коррекции. Частота задающего генератора стабилизируется кварцевым резонатором, а буферный усилитель обеспечивает развязку.
Возбудитель передатчика может быть выполнен по принципам построения синтезаторов сетки частот.
34,35,36 Фазовая модуляция цифровыми сигналами
Высокочастотный ФМ сигнал во временной области представляет собой синусоидальное колебание с постоянной частотой, постоянной амплитудой и переменной фазой.
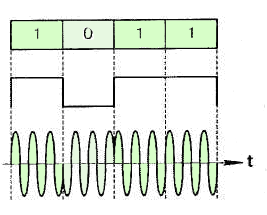
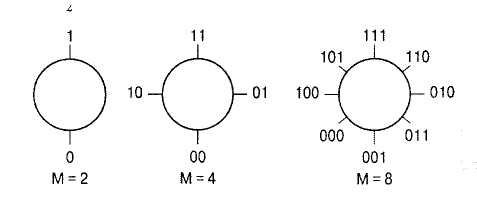
Диаграмма состояний ФМ колебания определяет зависимость абсолютного значения фазы сигнала (или приращения фазы при относительной фазовой модуляции) от передаваемого символа цифрового сообщения. Графически она представляет собой тригонометрический круг, по которому на равном угловом расстоянии расположены возможные значения фазы Qk. Каждому значению символа цифрового сообщения ставится в соответствие значение фазы Qk.
Диаграммы состояний для бинарной (М = 2), четырехуровневой (М = 4) и восьмиуровневой (М = 8) фазовой модуляции при начальном угле θ0 = 0 .
Формально соотношение между значениями фазы модулированного сигнала и символами цифрового сообщения может быть произвольным; но практически придерживаются кода Грея.
34 Фазовая модуляция цифровыми сигналами. Бинарная фазовая модуляция. Бинарная фазовая модуляция
Бинарная фазовая модуляция (Binary Phase Shift Keying - BPSK) осуществляется двухуровневым модулирующим сигналом (М = 2). Комплексная огибающая BPSK-сигнала на каждом k-ом символьном интервале имеет следующий вид:
gk(t)=cos[θ0+π wk(t)] + jsin[θ0+π wk(t)],
где wk(t) – двоичный нормированный сигнал.
Из формулы следует, что комплексная огибающая BPSK-сигнала при использовании модулирующего сигнала с прямоугольными импульсами представляет собой бинарный полярный цифровой сигнал.
Высокочастотный ФМ сигнал во временной области представляет собой синусоидальное колебание с постоянной частотой, постоянной амплитудой и переменной фазой.
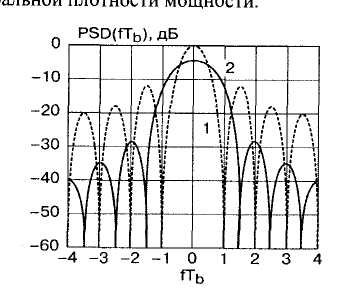
Спектральная плотность мощности BPSK-сигнала.
Использование модулирующего сигнала с более гладкой формой импульсов (треугольного – кривая 2) привело к расширению главного лепестка и уменьшению амплитуды боковых лепестков в спектральной плотности мощности.
35Фазовая модуляция цифровыми сигналами. Квадратурная фазовая модуляция.
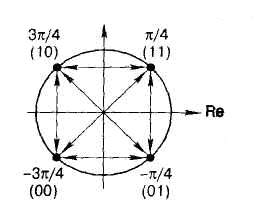
Квадратурная фазовая модуляция (Quadrature Phase Shift Keying - QPSK) является четырехуровневой фазовой модуляцией (М = 4), при которой фаза высокочастотного колебания может принимать 4 различных значения с шагом, кратным π/2.
Соотношение между абсолютными величинами фазы модулированного колебания из множества {±π/4, ±Зπ/4} и множеством символов (дибитов) цифрового сообщения {00, 01, 10, 11} устанавливается в каждом конкретном случае стандартом на радиоканал и фиксируется в диаграмме фазовых состояний.
Каждому значению фазы модулированного сигнала соответствуют два бита информации, и поэтому изменение модулирующего сигнала при QPSK-модуляции происходит в 2 раза реже, чем при BPSK-модуляции при одинаковой скорости передачи информации. Спектральная плотность мощности многоуровневого сигнала совпадает со спектральной плотностью мощности бинарного сигнала при замене битового интервала Тb на символьный интервал Ts.
Для четырехуровневой модуляции Ts = 2Тb. Таким образом, спектральная плотность мощности QPSK-сигнала (для положительных частот) при модулирующем сигнале с импульсами прямоугольной формы определяется выражением
Из формулы видно, что расстояние между первыми нулями спектральной плотности мощности сигнала QPSK равно Δf = 1/Тb, что в 2 раза меньше, чем для сигнала BPSK. Другими словами, спектральная эффективность квадратурной модуляции QPSK в 2 раза выше, чем бинарной модуляции BPSK.