
- •23.Основные булевы функции двух переменных.
- •24.Нормальные формы. Сднф. Скнф.
- •25.Алгоритм построения сднф.
- •26.Полнота системы булевых функций. Примеры полных систем.
- •27 Полином Жегалкина. Полная система для его построения
- •28.Теорема Поста. Замкнутые классы функций. Примеры.
- •33. Виды графов. Двудольные графы. Операции над графами
- •34. Способы представления графов в компьютере
- •35 Орграфы и бинарные отношения. Транзитивные зависимости
- •36 Свободные деревья. Лес. Основные свойства деревьев
- •37 Упорядоченные и бинарные деревья
- •38.Представление деревьев в компьютере.
- •40.ДеревоСортировки.АссоциативныйМассив.Сравнение производительности
- •41.АлгоритмыВставки,удаленияИПоискавДеревеСортировки Поиск элемента (find)
- •Добавление элемента (insert)
- •Удаление узла (remove)
- •Обход дерева (traverse)
- •42.АвЛдеревья.Балансировка
- •43.КратчайшийОстов.АлгоритмКрускала
- •44.КратчайшийОстов.АлгоритмПрима
- •45.ЗадачаНахожденияКратчайшегоПутиНаГрафе.АлгоритмБеллманаФорда
- •Граф с отрицательными циклами
- •46.Алгори́тм Де́йкстры
- •47.АлгоритмА-star
- •51. Алгоритм Форда-Фалкерсона.
- •52. Алгоритм проталкивания предпотока
- •53. Эйлеров цикл. Алгоритм построения.
- •54. Гамильтонов цикл. Задача коммивояжера.
- •55. Раскраска графов. Хроматическое число. Алгоритм раскрашивания
- •56. Планарные графы. Задача укладки графа на поверхность. Примеры планарных графов.
- •Укладка на поверхности
- •57.Теорема о раскарске планарных графов
1)Множества
и его элементы




![]()


2)Мощность Множеств. Равномощные множества. Конечные и бесконечные
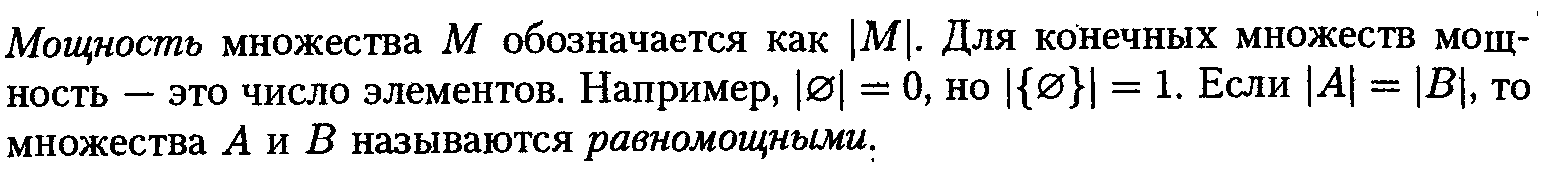
Конечное множество состоит из конечного числа элементов, например, множество страниц в книге, множество учеников в школе и т.д.
Бесконечное
множество
состоит
из
бесконечного
числа
элементов,
т.е.
это
множество,
которое не
является
ни конечным, ни пустым. Примеры: множество
действительных чисел,
множество
точек
плоскости,
множество
атомов
во
Вселенной
и
т.д.
![]()
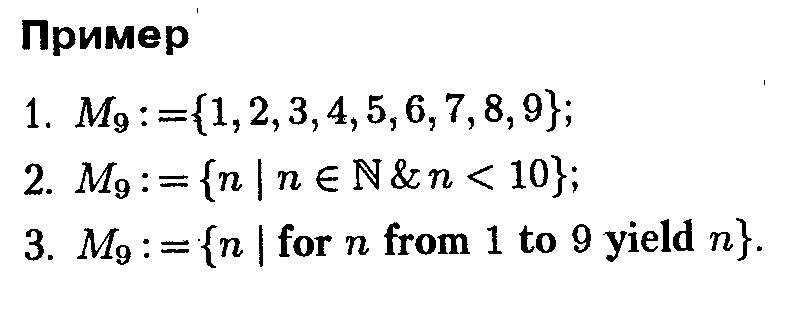
3.Мощность множества. Добавление и удаление элементов. Вычисление мощности. Булеан
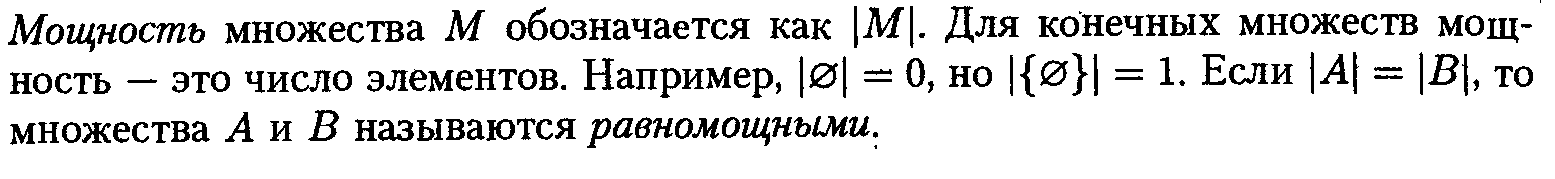

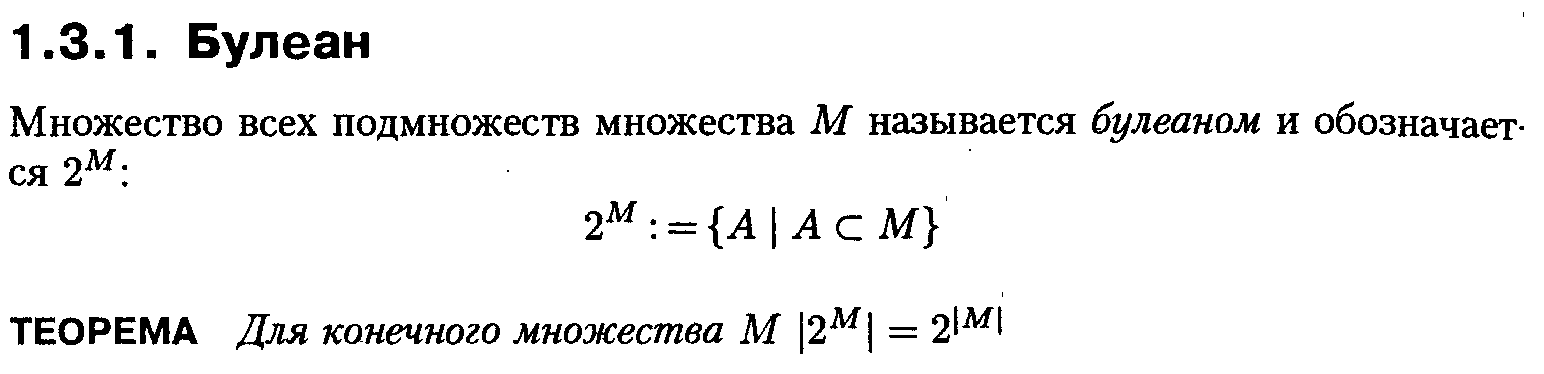
Число
подмножеств конечного множества,
состоящего из ![]() элементов,
равно
элементов,
равно ![]() .
.
4.Операции над множествами. Диаграммы Венна. Разбиения и покрытия множеств

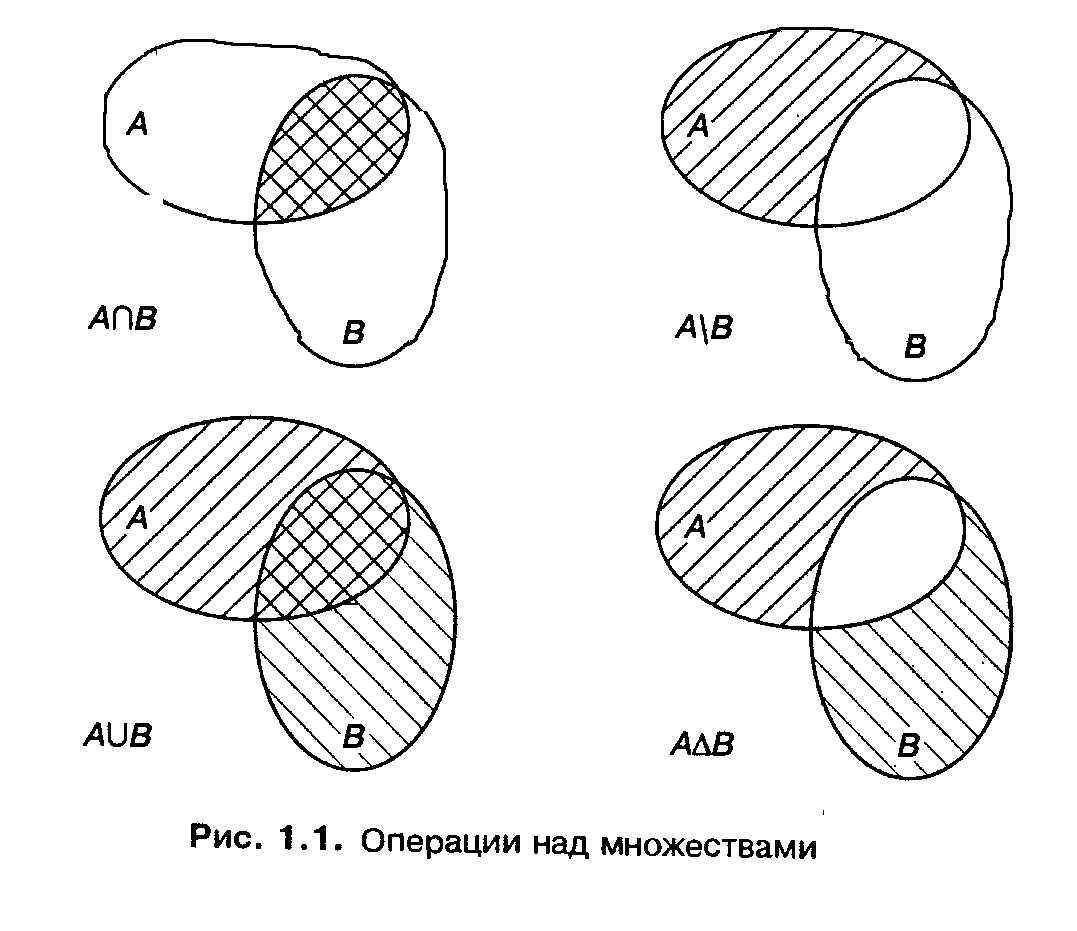
![]()

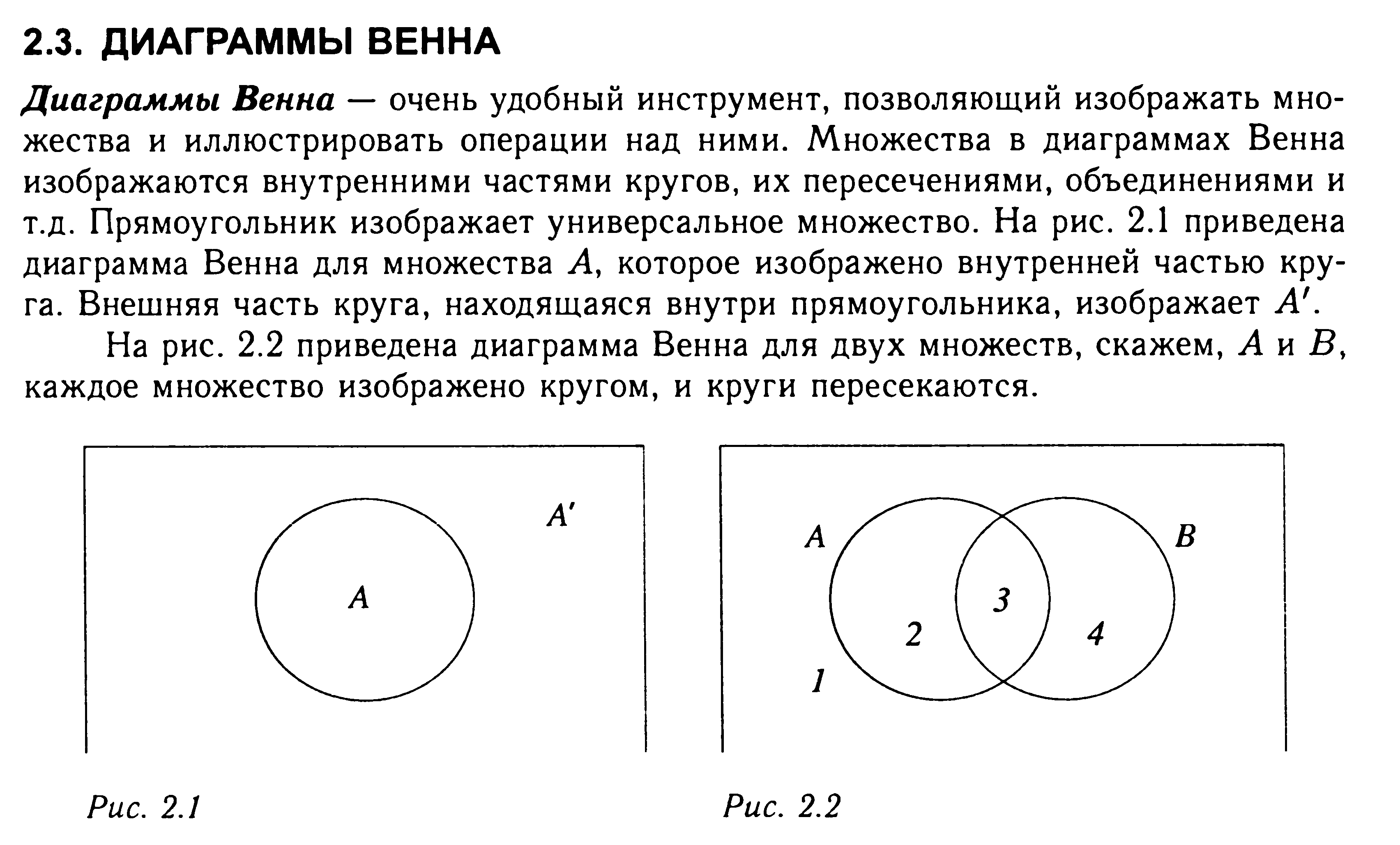
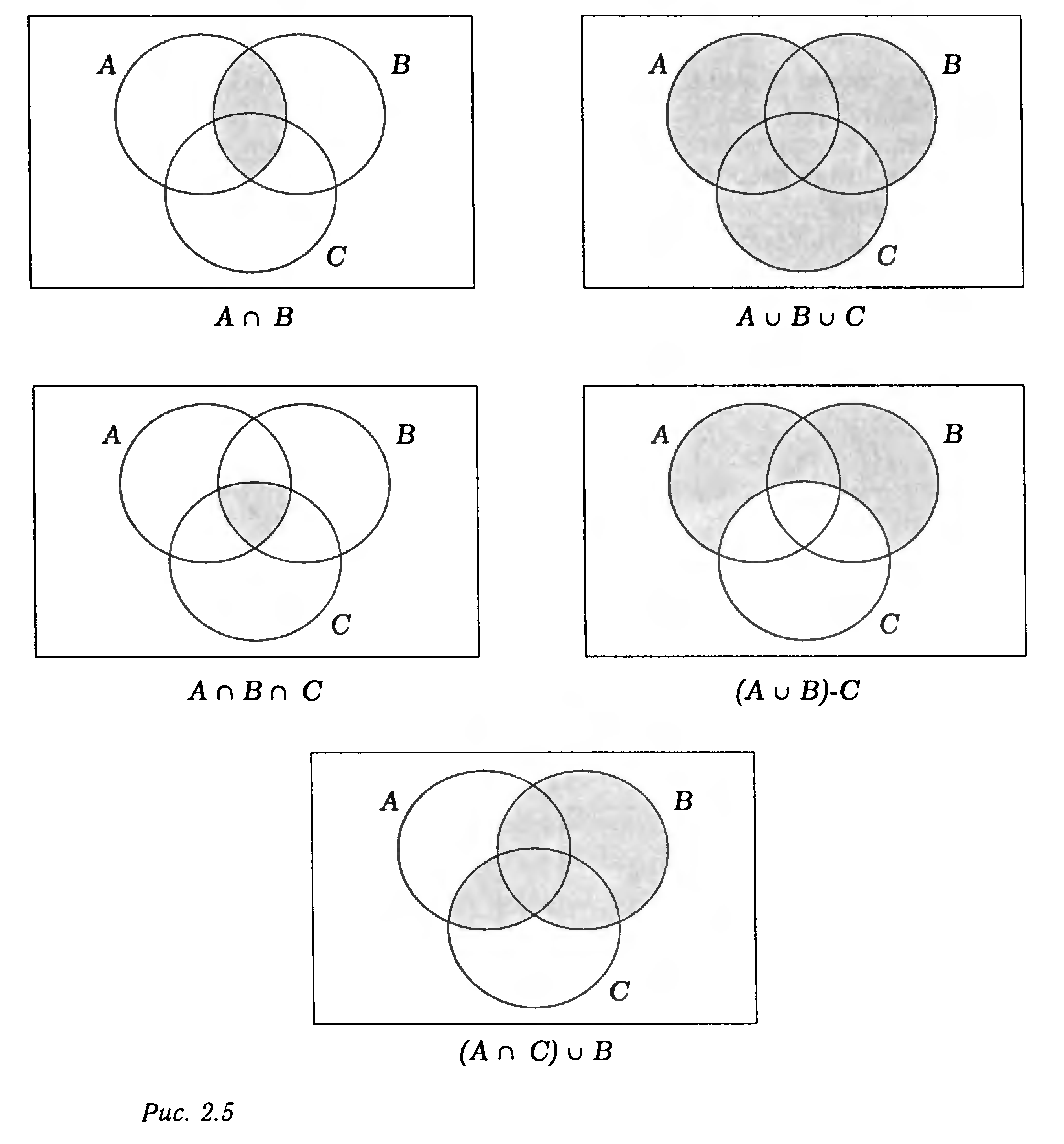
5.Свойства операций над множествами (не меньше 8)

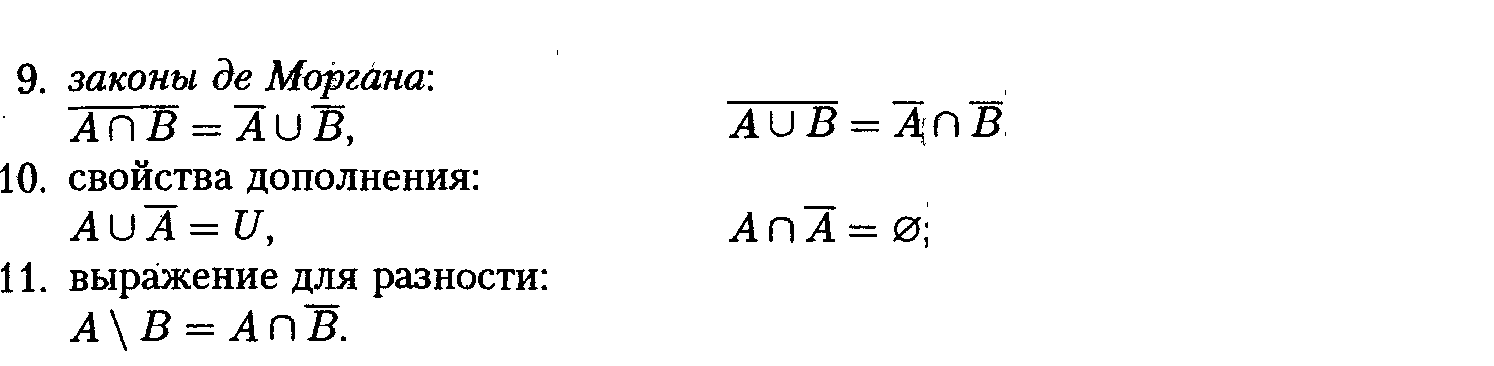
6.Представление множеств в программах. Генерация всех подмножеств (2 способа)






7.Представление
множеств упорядоченными списками.
Проверка включения. Операция объединения
и пересечения.



8.Отношения. Упорядоченные пары. Прямое произведение множеств.



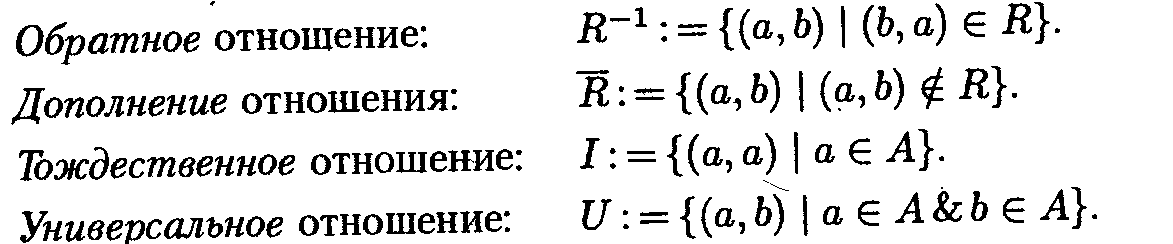
9.Бинарные отношения. Основные определения и виды отношений. Композиция отношений.


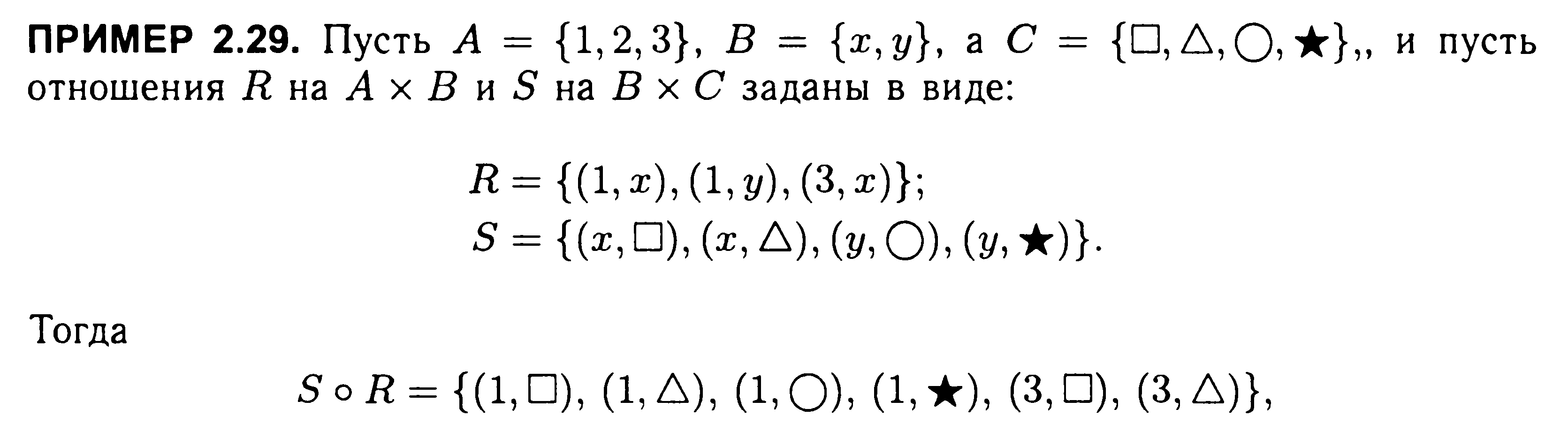
10.Свойства отношений(6 штук). Представление отношений в компьютере.


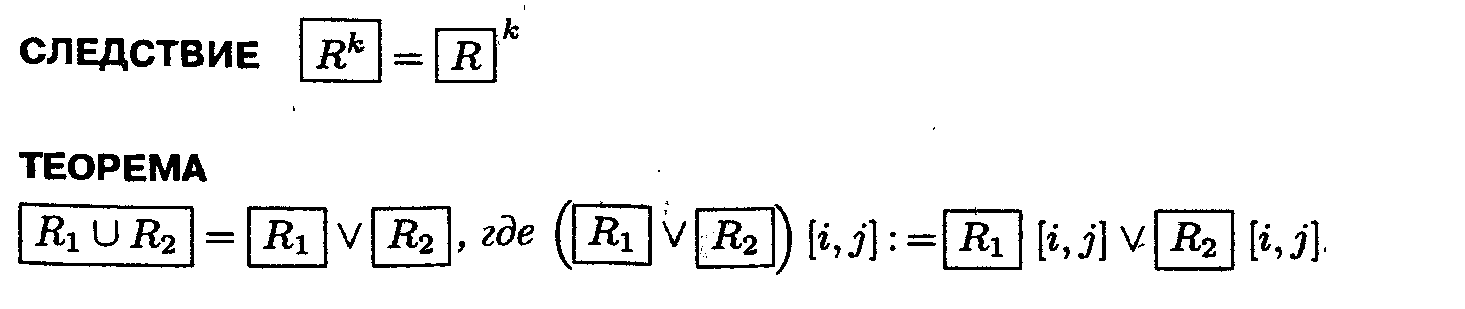
11.Замыкание отношений. Алгоритм построения транзитивного замыкания.
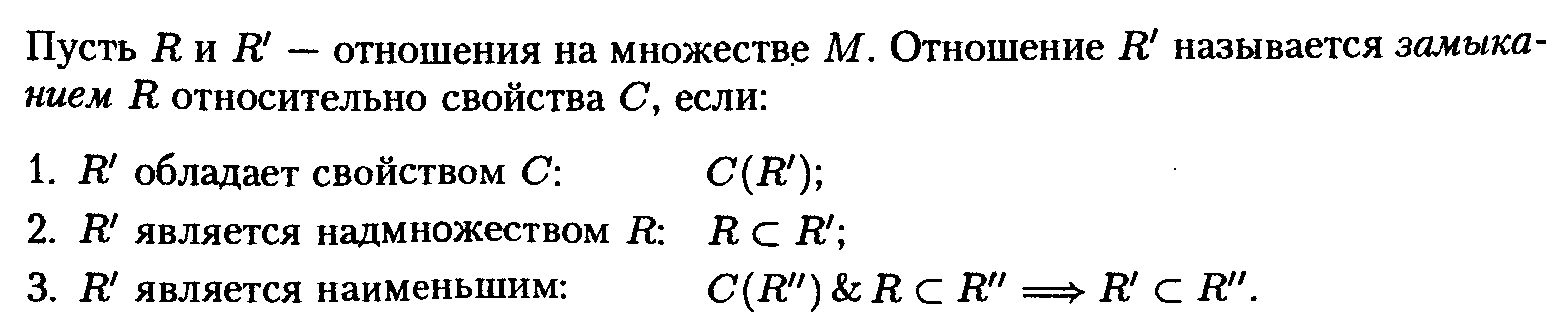
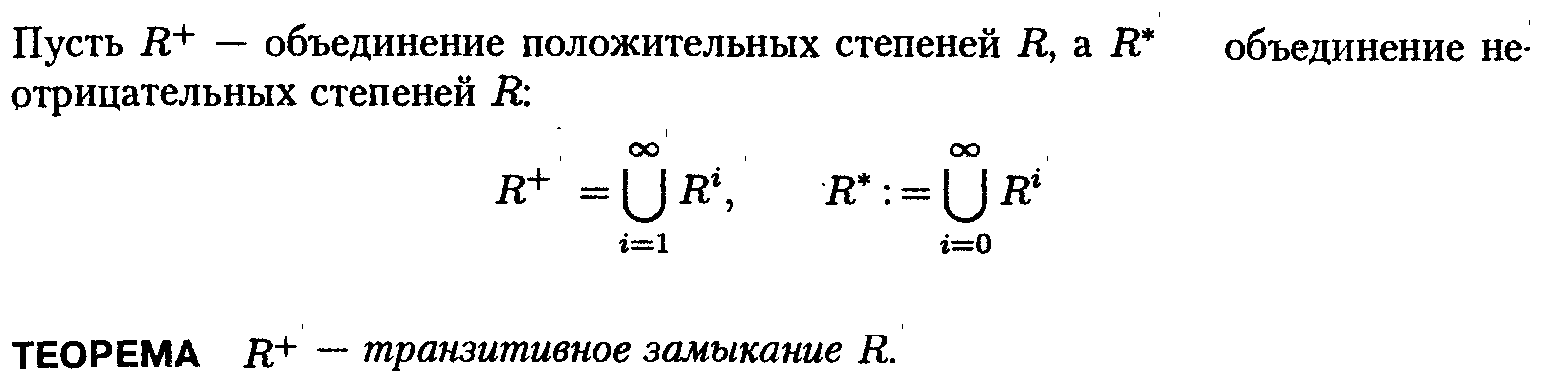
![]()
Пусть
на множестве ![]() задано
отношение
задано
отношение ![]() .
Видно, что отношение
.
Видно, что отношение ![]() не симметрично,
не рефлексивно и
не транзитивно.
Замыканием
относительно
свойства симметричности является
не симметрично,
не рефлексивно и
не транзитивно.
Замыканием
относительно
свойства симметричности является ![]() .
Замыканием
относительно
рефлексивности является
.
Замыканием
относительно
рефлексивности является ![]() .
Замыканием
относительно
транзитивности является множество
.
Замыканием
относительно
транзитивности является множество ![]() .
.

12.Функциональные
отношения. Инъекция, сюрьекция и биекция.

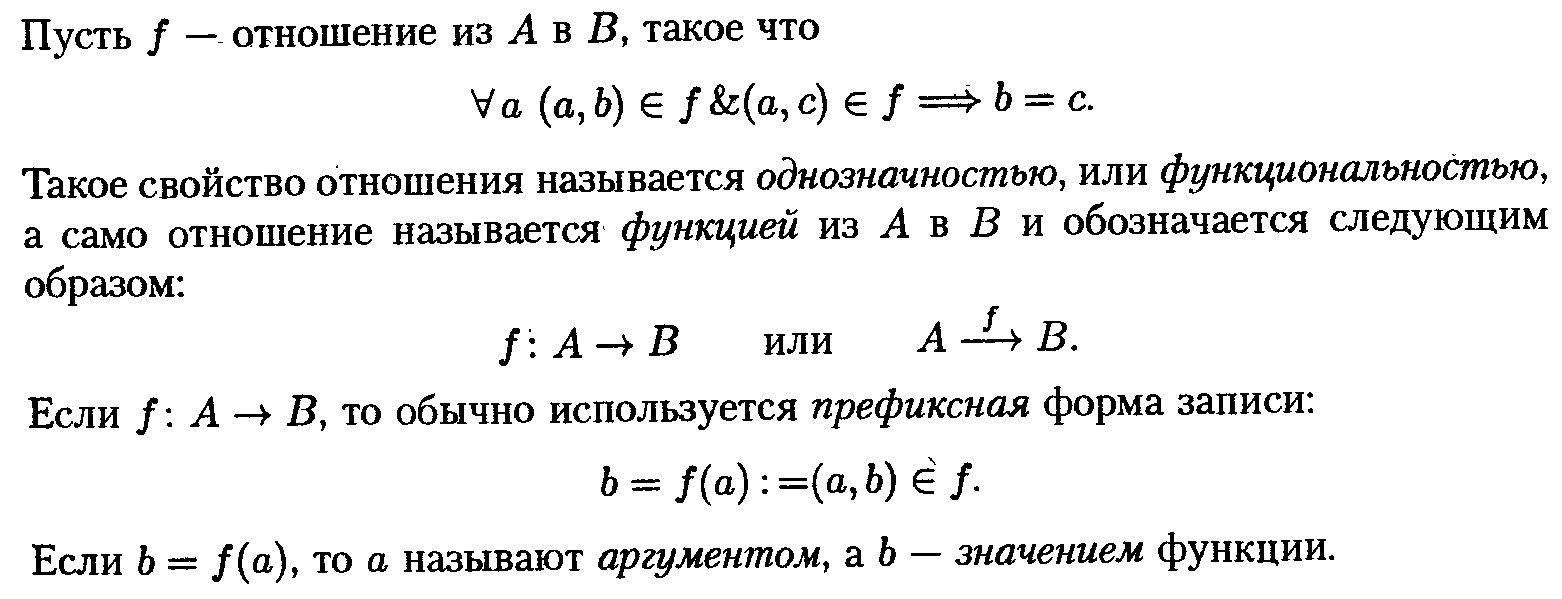
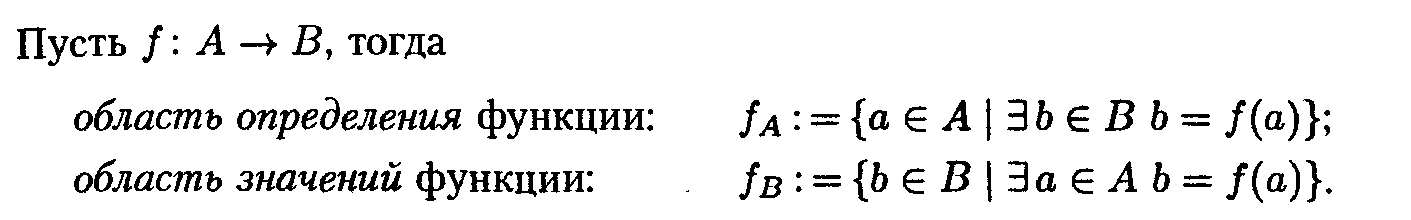
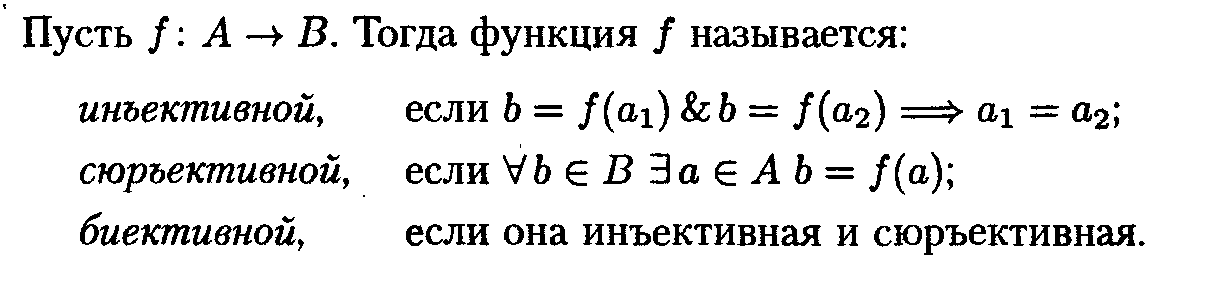


13.Отношение
эквивалентности. Классы эквивалентности.


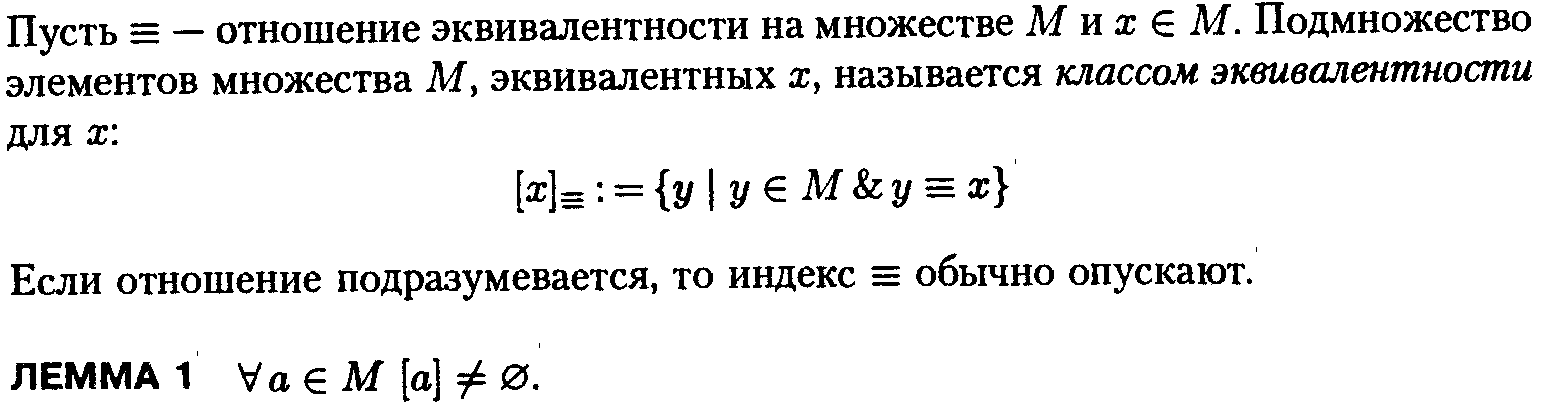
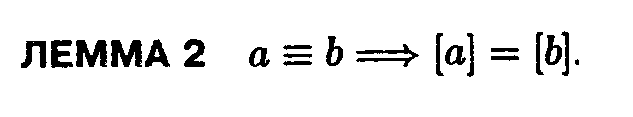
![]()

14.Отношение порядка. Частичный и полный порядок. Алгоритм топологической сортировки.




Поиск в глубину или обход в глубину (англ. Depth-first search, сокращенно DFS) — один из методов обхода графа. Алгоритм поиска описывается следующим образом: для каждой не пройденной вершины необходимо найти все не пройденные смежные вершины и повторить поиск для них.
Цвет: во
время обхода в глубину используется 3
цвета. Изначально все вершины белые.
Когда вершина обнаружена, красим ее в
серый цвет. Когда просмотрен список
всех смежных с ней вершин, красим ее в
черный цвет.
Думаю
будет проще рассмотреть данный алгоритм
на примере:
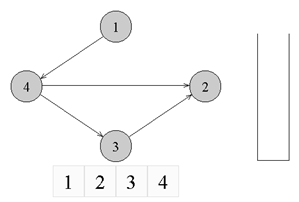 ↑
Имеем бесконтурный ориентированный
граф. Изначально все вершины белые, а
стек пуст. Начнем обход в глубину с
вершины номер 1.
↑
Имеем бесконтурный ориентированный
граф. Изначально все вершины белые, а
стек пуст. Начнем обход в глубину с
вершины номер 1.
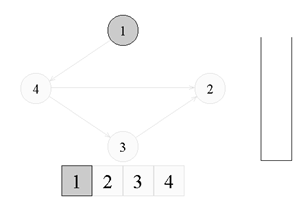 ↑
Переходим к вершине номер 1. Красим ее
в серый цвет.
↑
Переходим к вершине номер 1. Красим ее
в серый цвет.
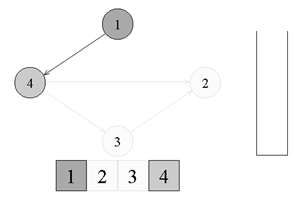 ↑
Существует ребро из вершины номер 1 в
вершину номер 4. Переходим к вершине
номер 4 и красим ее в серый цвет.
↑
Существует ребро из вершины номер 1 в
вершину номер 4. Переходим к вершине
номер 4 и красим ее в серый цвет.
 ↑
Существует ребро из вершины номер 4 в
вершину номер 2. Переходим к вершине
номер 2 и красим ее в серый цвет.
↑
Существует ребро из вершины номер 4 в
вершину номер 2. Переходим к вершине
номер 2 и красим ее в серый цвет.
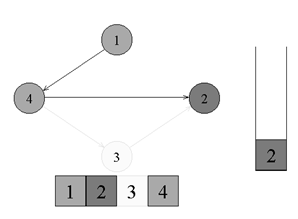 ↑
Из вершины номер 2 нет рёбер, идущих не
в черные вершины. Возвращаемся к вершине
номер 4. Красим вершину номер 2 в черный
цвет и кладем ее в стек.
↑
Из вершины номер 2 нет рёбер, идущих не
в черные вершины. Возвращаемся к вершине
номер 4. Красим вершину номер 2 в черный
цвет и кладем ее в стек.
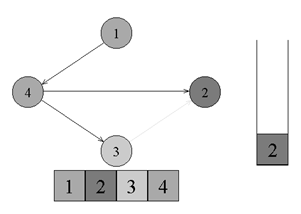 ↑
Существует ребро из вершины номер 4 в
вершину номер 3. Переходим к вершине
номер 3 и красим ее в серый цвет.
↑
Существует ребро из вершины номер 4 в
вершину номер 3. Переходим к вершине
номер 3 и красим ее в серый цвет.
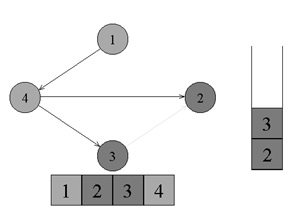 ↑
Из вершины номер 3 нет рёбер, идущих не
в черные вершины. Возвращаемся к вершине
номер 4. Красим вершину номер 3 в черный
цвет и кладем ее в стек.
↑
Из вершины номер 3 нет рёбер, идущих не
в черные вершины. Возвращаемся к вершине
номер 4. Красим вершину номер 3 в черный
цвет и кладем ее в стек.
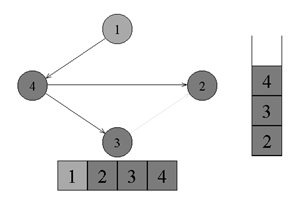 ↑
Из вершины номер 4 нет рёбер, идущих не
в черные вершины. Возвращаемся к вершине
номер 1. Красим вершину номер 4 в черный
цвет и кладем ее в стек.
↑
Из вершины номер 4 нет рёбер, идущих не
в черные вершины. Возвращаемся к вершине
номер 1. Красим вершину номер 4 в черный
цвет и кладем ее в стек.
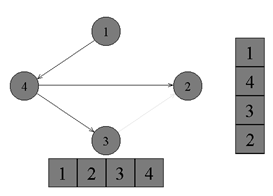 ↑
Из вершины номер 1 нет рёбер, идущих не
в черные вершины. Красим её в черный
цвет и кладем в стек. Обход точек
закончен.
↑
Из вершины номер 1 нет рёбер, идущих не
в черные вершины. Красим её в черный
цвет и кладем в стек. Обход точек
закончен.
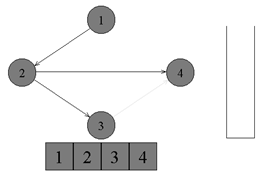 ↑
По очереди достаем все вершины из стека
и присваиваем им номера 1, 2, 3, 4 соответсвенно.
Алгоритм топологической сортировки
завершен. Граф отсортирован.
↑
По очереди достаем все вершины из стека
и присваиваем им номера 1, 2, 3, 4 соответсвенно.
Алгоритм топологической сортировки
завершен. Граф отсортирован.
15.Алгебра. Операции и носитель. Основные свойства операций(6 штук).
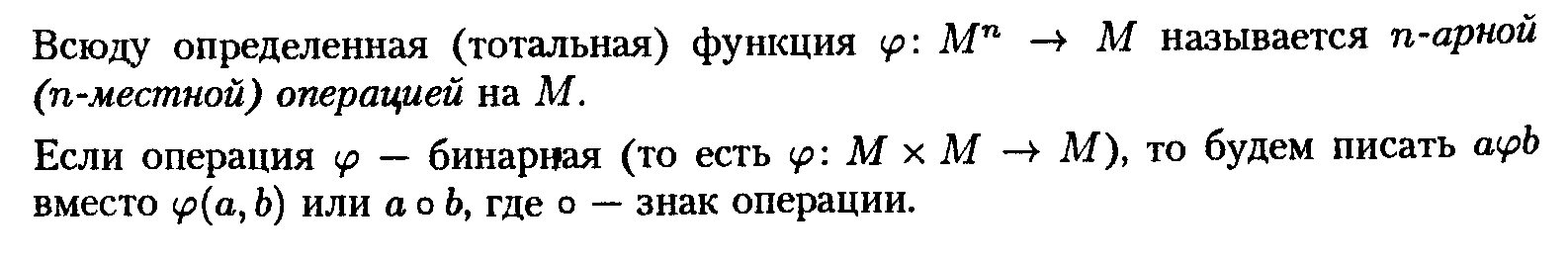

Алгебраическая
система (или алгебраическая
структура)
в универсальной
алгебре — множество ![]() (носитель)
с заданным на нём
набором операций и отношений (сигнатура),
удовлетворяющим некоторой системе аксиом.
Алгебраическая система с пустым
множеством отношений называется универсальной
алгеброй,
а система с пустым множеством операций —
моделью.
(носитель)
с заданным на нём
набором операций и отношений (сигнатура),
удовлетворяющим некоторой системе аксиом.
Алгебраическая система с пустым
множеством отношений называется универсальной
алгеброй,
а система с пустым множеством операций —
моделью.

16.Морфизмы. Гомоморфизмы. Изоморфизмы.


Гомоморфизм - это отображение алгебраической системы А, сохраняющее основные операции и основные соотношения.
Например,
рассмотрим группы ![]() ,
, ![]() .
Отображение
.
Отображение ![]() называется
гомоморфизмом групп
называется
гомоморфизмом групп ![]() и
и ![]() ,
если оно одну групповую операцию
переводит в другую:
,
если оно одну групповую операцию
переводит в другую: ![]() .
.
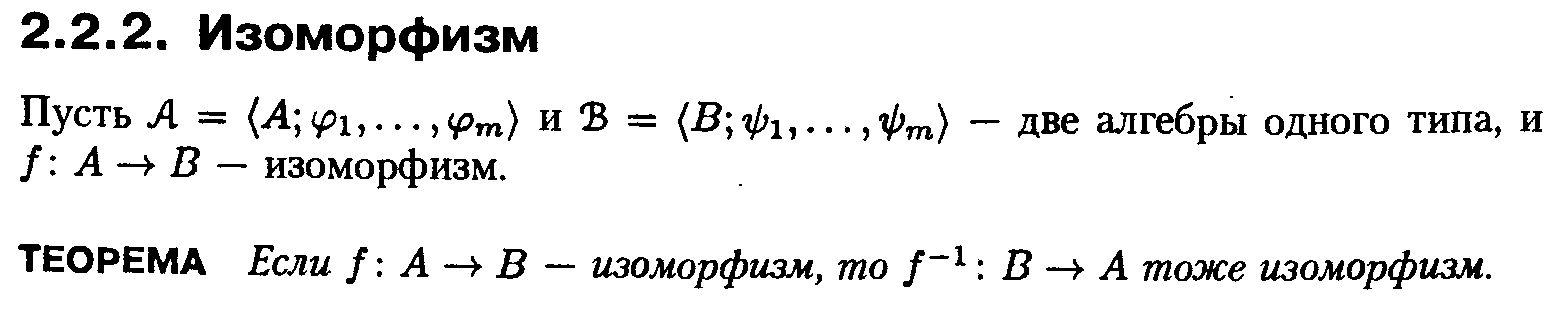

Пусть ![]() и
и ![]() —
поля. Биекция
—
поля. Биекция ![]() называется изоморфизмом,
если для любых
называется изоморфизмом,
если для любых ![]() выполняется
выполняется
 ,
,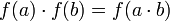 .
.
17.Алгебры
с одной операцией. Полугруппы. Моноиды

![]()
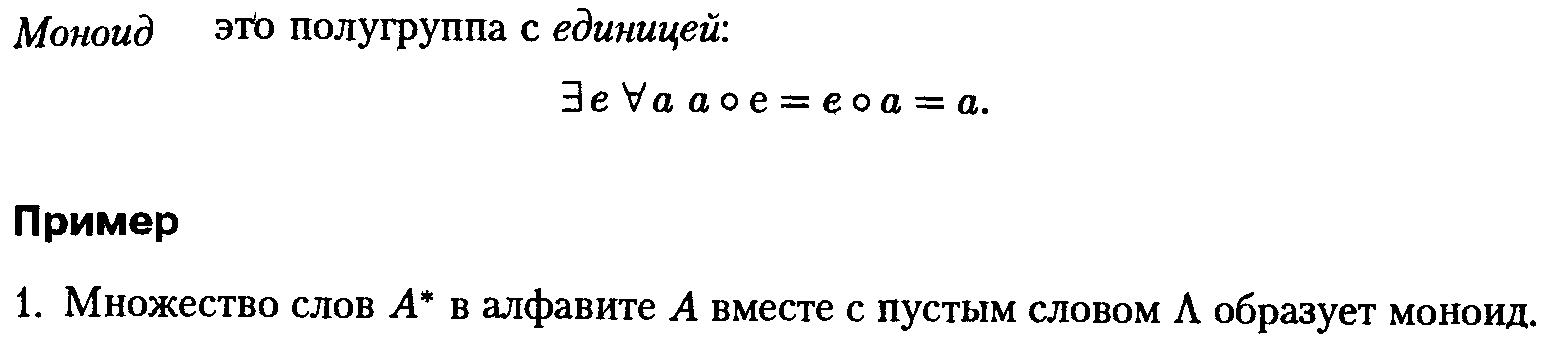
![]()
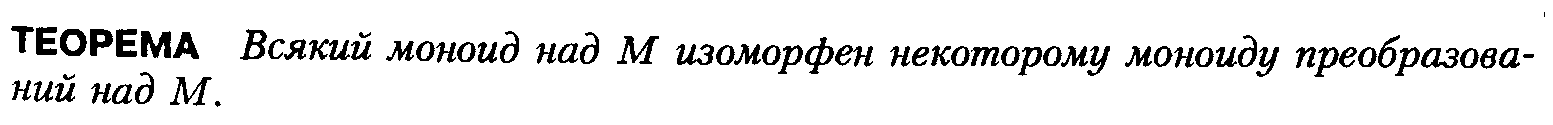
18.Группа. Основные свойства групп. Группа перестановок.
Непустое
множество
с
заданной на нём бинарной
операцией ![]() называется
группой
называется
группой ![]() ,
если выполнены следующие аксиомы:
,
если выполнены следующие аксиомы:
ассоциативность: ![]() ;
;
наличие нейтрального элемента:
![]() ;
;
наличие обратного элемента:
![]()
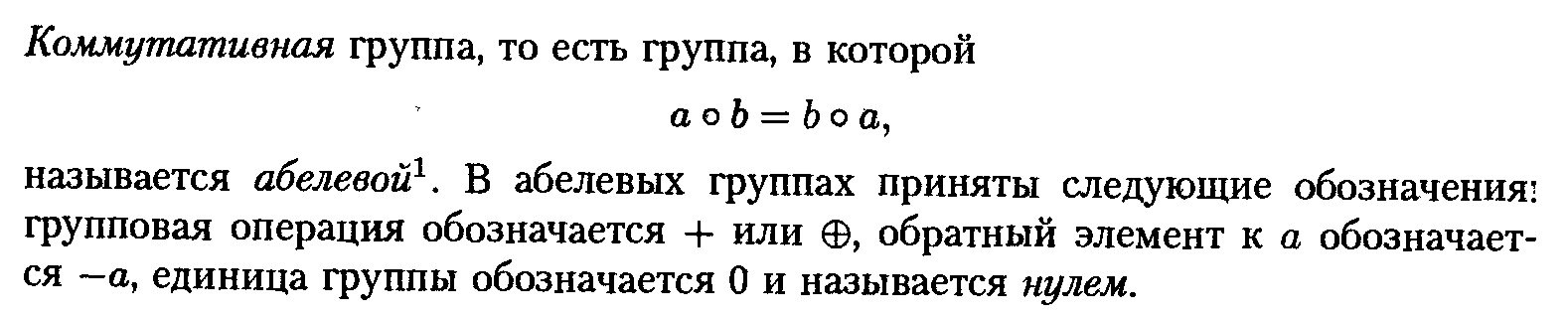
Примеры
Целые числа с операцией сложения.
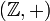 группа
с нейтральным элементом 0. Она является
абелевой.
группа
с нейтральным элементом 0. Она является
абелевой.
Положительные рациональные числа с операцией умножения. Произведение рациональных чисел — снова рациональное число, обратный элемент к рациональному числу представляется обратной дробью, имеется ассоциативность и единица.
Простейшие свойства
Обратный к данному элемент всегда определяется однозначно.
(a−1)−1 = a, aman = am+n, (am)n = amn.
(ab)−1 = b−1a−1.
Верны законы сокращения:
![]() ,
,
![]() .
.
Обратный элемент к нейтральному есть сам нейтральный элемент.
Группа содержит единственное решение x любого уравнения x · c = b или c · x = b; то есть в группе возможны однозначно определённые правое и левое «деление».
Пересечение двух подгрупп группы G есть подгруппа группы G.
Теорема Лагранжа: если G — группа конечного порядка g, то порядок g1 любой её подгруппы G1 является делителем порядка группы. Из этого следует, что и порядок любого элемента делит порядок группы.
Для определения числа подгрупп в группе используются теорема Лагранжа и теоремы Силова.
Симметрической группой множества X называется группа всех перестановок X (то есть биекций X →X) относительно операции композиции.
Симметрическая группа множества X обычно обозначается S(X). Если X = {1, 2,…, n}, то S(X) также обозначается через Sn.
Нейтральным
элементом в симметрической группе
является тождественная перестановка ![]() ,
определяемая как тождественное
отображение:
,
определяемая как тождественное
отображение:
![]() для
всех x из X.
для
всех x из X.
Свойства
При
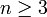 симметрическая
группа Sn некоммутативна.
симметрическая
группа Sn некоммутативна.При
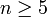 симметрическая
группа Sn является неразрешимой (и
напротив: при
симметрическая
группа Sn является неразрешимой (и
напротив: при 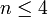 —
разрешимой).
—
разрешимой).В случае, если X конечно, число элементов S(X) равно n! (факториал n), где n — число элементов X. В частности,
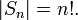
Каждая конечная группа G изоморфна некоторой подгруппе группы S(G) (теорема Кэли).
Симметрическая группа Sn допускает следующее задание:
![]()
(Можно
считать, что ![]() переставляет i и i+1.)
переставляет i и i+1.)
19.Кольца. Области целостности. Поля.


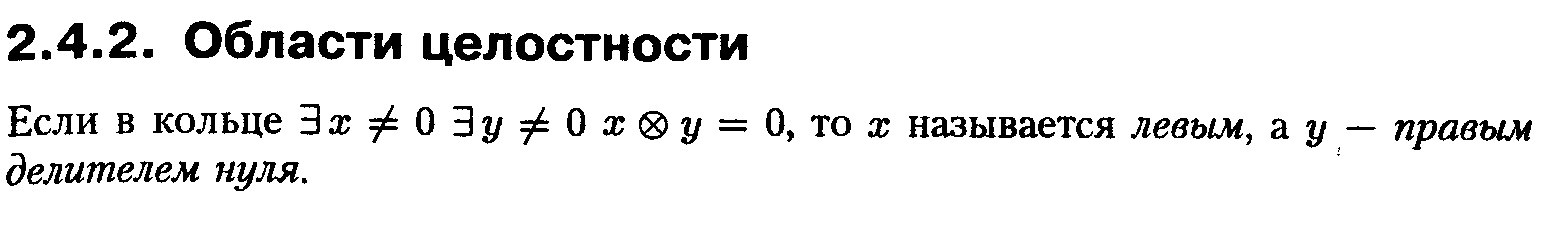



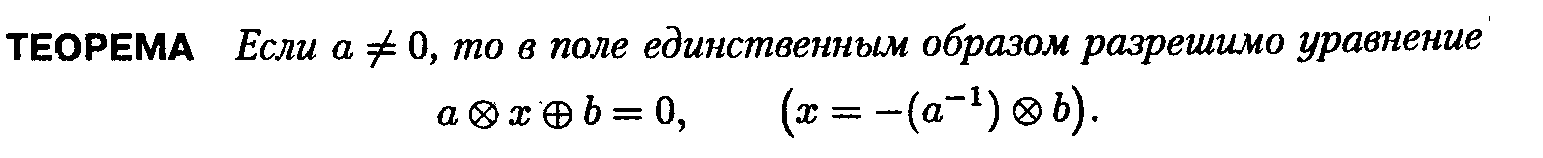
20.Векторное пространство. Нуль-вектор. Линейные комбинации. Базис и размерность пространства.

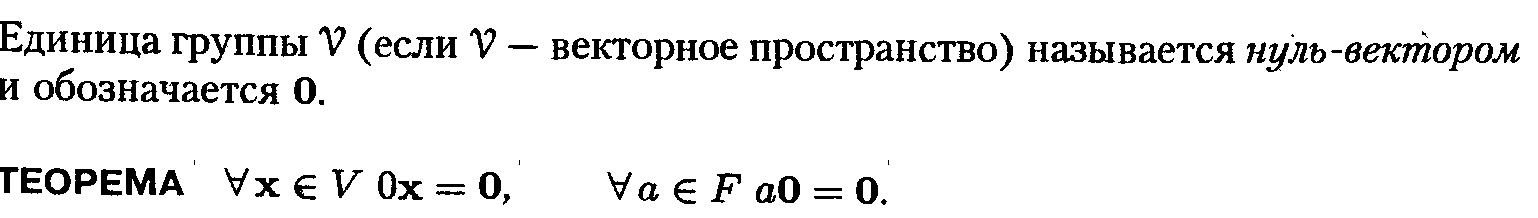
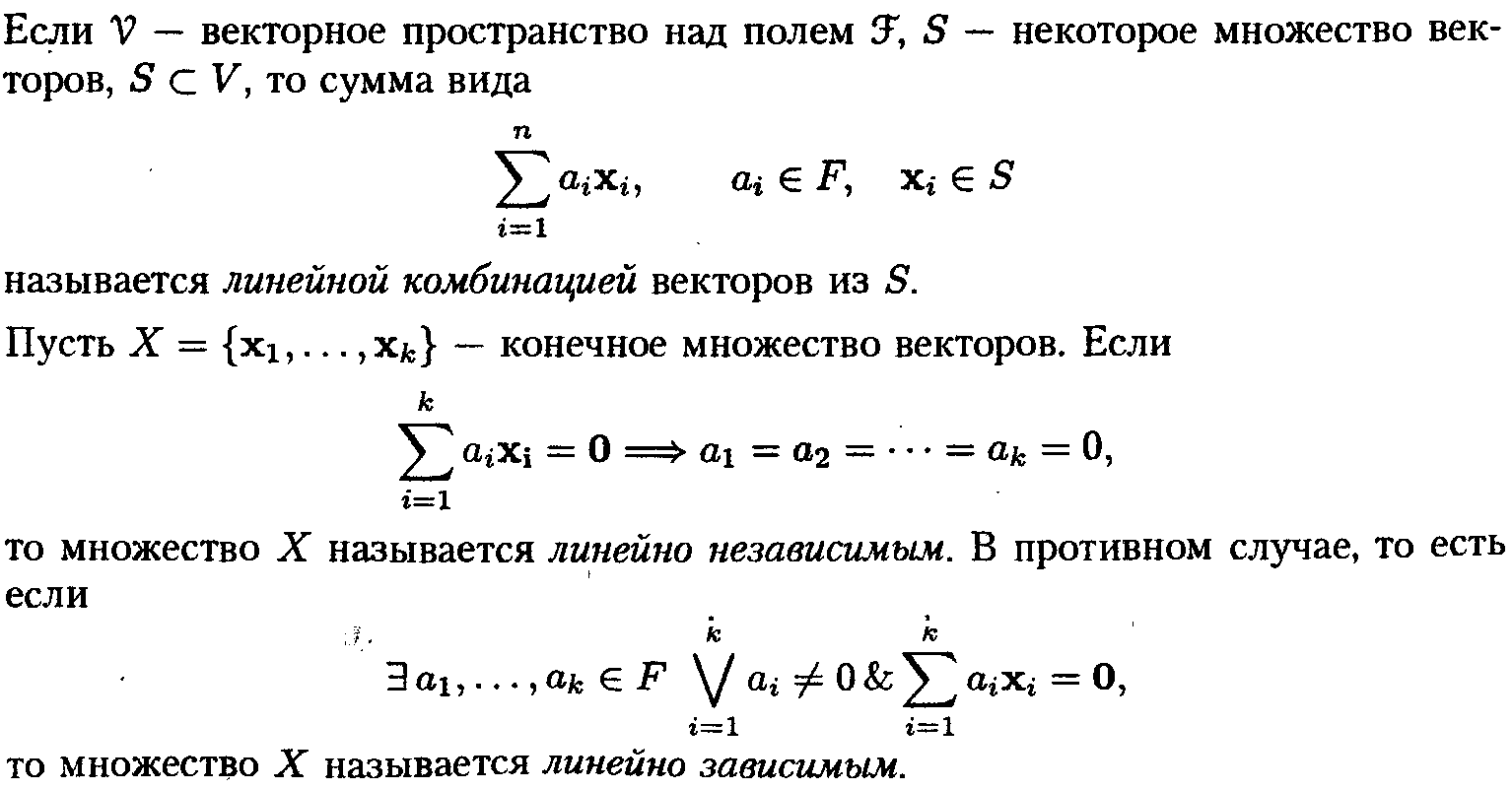
![]()

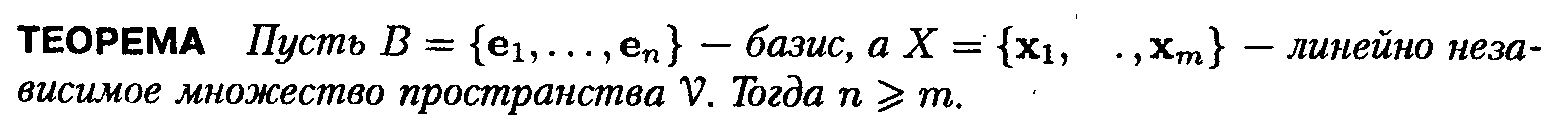
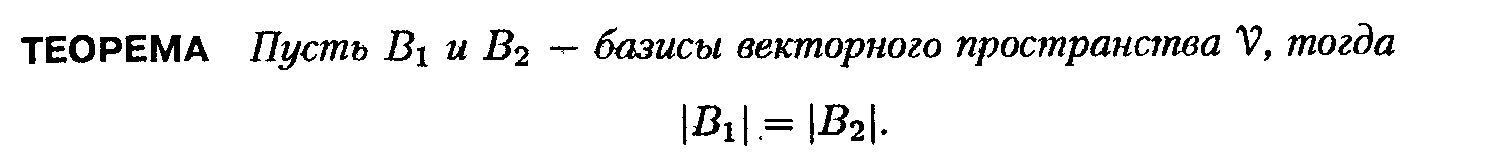

21.Решетка. Ограниченная решетка. Булева алгебра (Доказательство того, что булева алгебра является решеткой)


![]()
![]()


22.Функции алгебры логики. Множество булевых функций. Существенные и несущественные переменные. Булевы функции одной переменной.
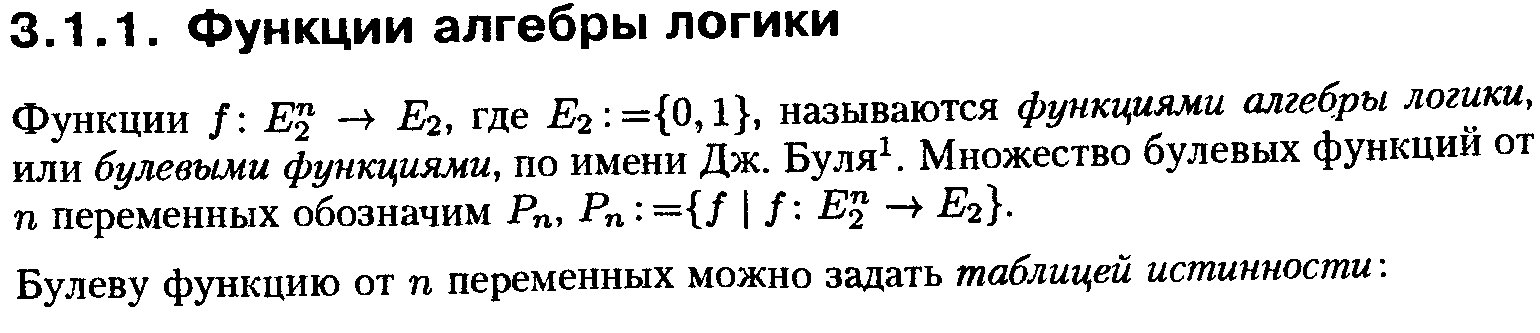

Бу́лева
фу́нкция (или логи́ческая
функция,
или функция
а́лгебры ло́гики)
от n переменных —
в дискретной
математике —
отображение Bn → B,
где B =
{0,1} — булево
множество.
Элементы булева множества 1 и 0 обычно
интерпретируют как логические значения
«истинно» и «ложно», хотя в общем случае
они рассматриваются как формальные
символы, не несущие определённого
смысла. Неотрицательное целое
число n называют арностью или
местностью функции, в случае n =
0 булева функция превращается в булеву
константу.
Элементы декартова
произведения Bn называют булевыми
векторами.
Множество всех булевых функций от любого
числа переменных часто обозначается P2,
а от n переменных — P2(n).
Булевы функции названы так по фамилии
математика Джорджа
Буля.
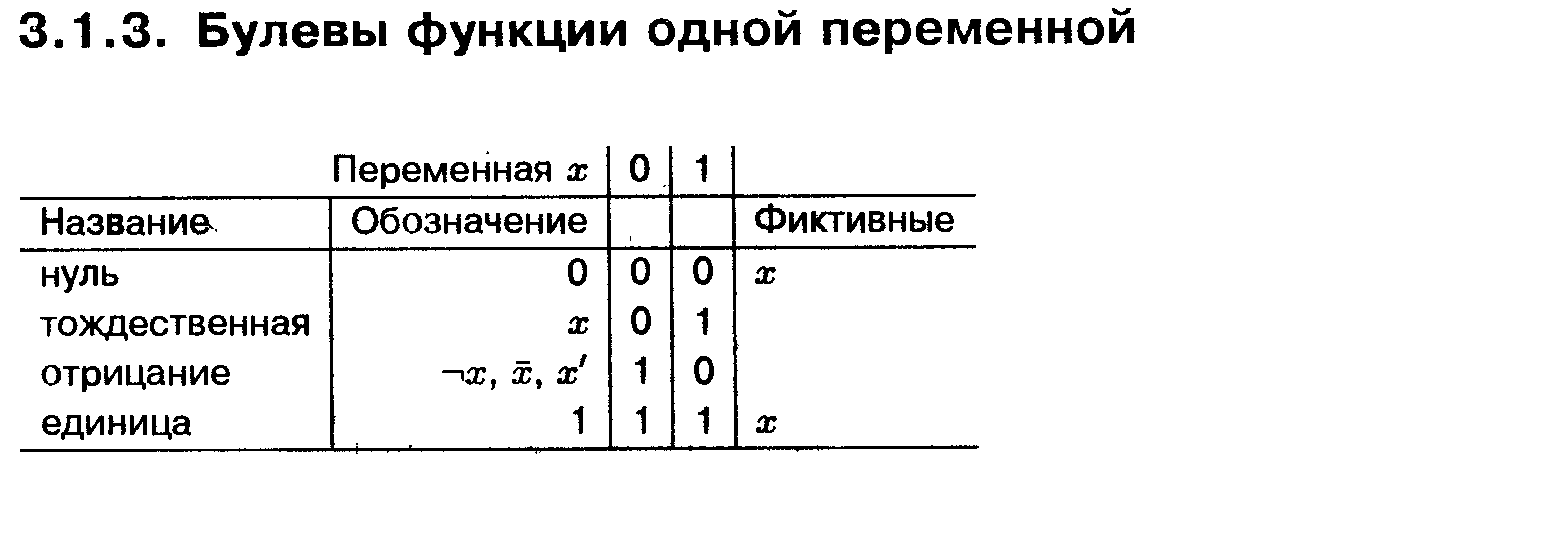
23.Основные булевы функции двух переменных.
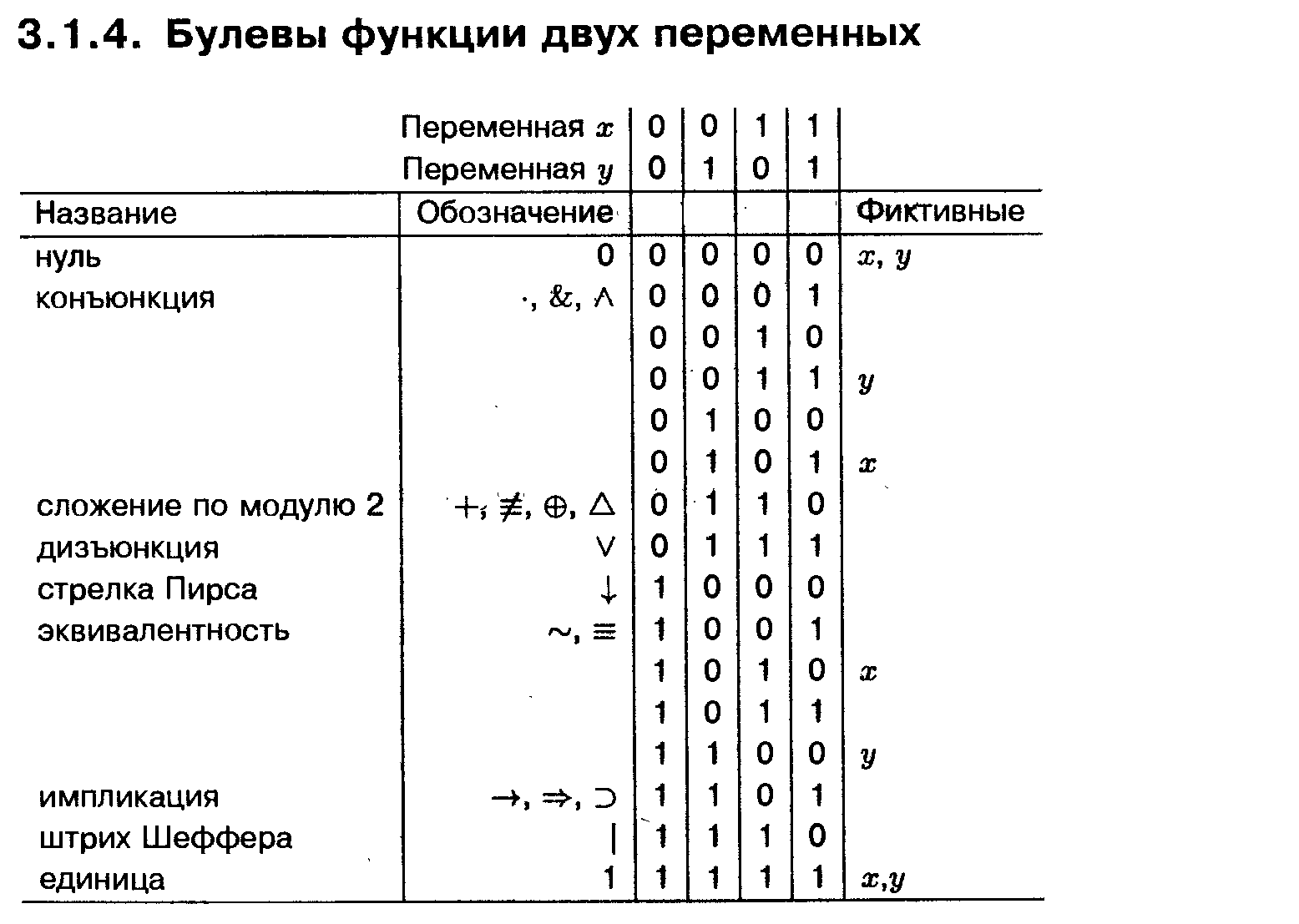
24.Нормальные формы. Сднф. Скнф.
 СДНФ
(Совершенная Дизъюнктивная Нормальная
Форма) —
это такая ДНФ,
которая удовлетворяет трём условиям:
СДНФ
(Совершенная Дизъюнктивная Нормальная
Форма) —
это такая ДНФ,
которая удовлетворяет трём условиям:
в ней нет одинаковых элементарных конъюнкций
в каждой конъюнкции нет одинаковых пропозициональных букв
каждая элементарная конъюнкция содержит каждую пропозициональную букву из входящих в данную ДНФ пропозициональных букв, причем в одинаковом порядке.
Для любой функции алгебры логики существует своя СДНФ, причем единственная.
Пример нахождения СДНФ
Для того, чтобы получить СДНФ функции, требуется составить её таблицу истинности.
|
|
|
|
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
В ячейках строки́ отмечаются лишь те комбинации, которые приводят логическое выражение в состояние единицы.
Далее рассматриваются значения переменных при которых функция равна 1. Если значение переменной равно 0, то она записывается с инверсией. Если значение переменной равно 1, то без инверсии.
Первый столбец содержит 1 в указанном поле. Отмечаются значения всех четырёх переменных, это:
= 0
= 0
= 0
= 0
Нулевые
значения — тут все переменные представлены
нулями — записываются в конечном
выражении инверсией этой переменной.
Первый член СДНФ рассматриваемой функции
выглядит так: ![]() Переменные
второго члена:
Переменные
второго члена:
= 0
= 0
= 0
= 1
в
этом случае будет представлен без
инверсии: ![]()
Таким образом анализируются все ячейки . Совершенная ДНФ этой функции будет дизъюнкцией всех полученных членов (элементарных конъюнкций).
Совершенная ДНФ этой функции:
![]()
![]()
![]()
![]()
![]()
![]()
СКНФ (Совершенная Конъюнктивная Нормальная Форма) — это такая КНФ, которая удовлетворяет трём условиям:
в ней нет одинаковых элементарных дизъюнкций
в каждой дизъюнкции нет одинаковых пропозициональных букв
каждая элементарная дизъюнкция содержит каждую пропозициональную букву из входящих в данную КНФ пропозициональных букв.
Пример нахождения СКНФ
Для того, чтобы получить СКНФ функции, требуется составить её таблицу истинности
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
В ячейках строки́ отмечаются лишь те комбинации, которые приводят логическое выражение в состояние нуля.
Четвертый столбец содержит 0 в указанном поле. Отмечаются значения всех четырёх переменных, это:
= 0
= 0
= 1
= 1
В
дизъюнкцию записывается переменная
без инверсии если она в наборе равна 0
и с инверсией если она равна 1. Первый
член СКНФ рассматриваемой функции
выглядит так: ![]()
![]()
![]()
![]()
Остальные члены СКНФ составляются по аналогии.
