Рассмотрим функцию . Найдем ее приращение :

.

Следовательно, приращение функции можно рассматривать как сумму двух слагаемых: первого , линейного относительно , и второго , нелинейного относительно . При оба слагаемых являются бесконечно малыми, но второе слагаемое стремится к нулю быстрее:

.

Поэтому при малых приращениях функции можно считать приближенно равным его линейной части

Линейная часть приращения называется главной часть приращения функции. Пусть приращение функции в точке можно представить в виде:

( ** )

где - приращение аргумента, А - постоянная величина, - бесконечно малая функция более высокого порядка малости, чем , т.е. .

Если приращение функции в точке может быть представлено по формуле ( ** ), то главная часть приращения функции , пропорциональная приращению аргумента называется дифференциалом этой функции и обозначается .

Отбросив в формуле ( ** ) второе слагаемое при малых , получим приближенное равенство .

Теорема. Если функция имеет в точке дифференциал, то она имеет в этой точке производную.

Доказательство.

. Т.к. , то производная существует и равна A.

Отсюда получаем выражение для дифференциала.

Теорема. Если функция имеет в точке производную, то она имеет в этой точке дифференциал.

Геометрический смысл дифференциала.

Проведем к графику функции в точке касательную и обозначим через ее угол с осью ox.

Рассмотрим ординату этой касательной для точки . Отрезок NP назовем приращением ординаты касательной. Из следует: .

Покажем, что этот отрезок равен дифференциалу .

Т.к. то .

Т.о., дифференциал функции в точке равен приращению ординаты касательной.

Производная как отношение дифференциалов

Рассмотрим функцию . Ее дифференциал равен

Будем считать, что дифференциал независимой переменной равен ее приращению:

Тогда выражение для дифференциала примет вид: .

Разделив обе части равенства на , получим т.е. производная функции равна отношению ее дифференциала к дифференциалу независимой переменной.

Дифференциал суммы, произведение, частного функций. Дифференциал сложной функции

Пусть и – дифференцируемые функции.

Тогда справедливы формулы:

Пусть и – дифференцируемые функции. Рассмотрим сложную функцию . Тогда . Т.к. , то

.

Таким образом доказана следующая теорема:

Теорема. Дифференциал сложной функции , где , имеет такой же вид , как и в том случае, когда аргумент является независимой переменной.

Свойство дифференциала сложной функции, выражаемое этой теоремой, называется инвариантностью формы дифференциала.

5. Применение дифференциала к приближенным вычислениям

Пусть известно значение функции и ее производной в точке .

Найдем значение функции в точке . Запишем приращение функции

С другой стороны, по определению дифференциала функции А т.к. ,то , откуда .

Пример. Вычислить приближенно .

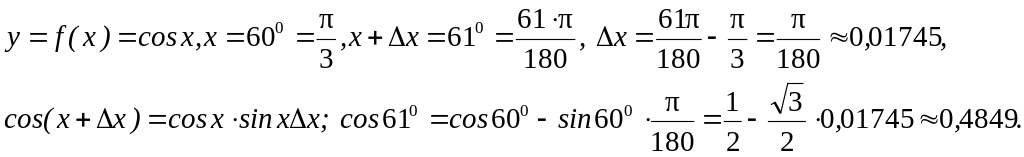
Некоторые теоремы о дифференцируемых функциях

Теорема Ферма. Пусть функция , определенная в интервале , принимает в некоторой точке этого интервала наибольшее или наименьшее значение.

Тогда если в точке существует производная, то она равна нулю.

Доказательство. Пусть для определенности -наибольшее значение функции в интервале По определению производной,

.

Т.к. в точке функция принимает наибольшее значение, то

.

Отсюда, если то и, следовательно, .

Если же то и .

Но т.к. производная не должна зависеть от знака , то .

Теорема Ролля. Если функция f(x) непрерывна на отрезке [a,в], дифференцируема во всех его внутренних точках и на концах отрезка обращается в нуль, т.е. f (a) = f (в) =0, то её производная обращается в нуль, хотя бы в одной внутренней точке этого отрезка.

Доказательство. Т.к. функция непрерывна на отрезке, то она достигает на нём своего наибольшего значения М и наименьшего значения m. Если Mm, то функция на постоянна, и, следовательно, её производная в любой точке отрезка. Пусть , тогда одно из этих чисел отлично от нуля, например, . Поэтому, если наибольшее значение М достигается в точке С, f(С)=M, то точка С должна быть внутренней точкой отрезка , т.е.

принадлежать интервалу , т.к. на концах отрезка f(a)=f(b)=0. Следовательно, по теореме Ферма =0.

Геометрически теорема Ролля означает, что если график непрерывной на отрезке и дифференцируемой внутри него функции пересекает ось ОХ в двух точках , то найдётся хотя бы одна точка С: , для которой касательная к графику параллельна оси абсцисс.

Теорема Лагранжа. Если функция f(x) непрерывна на отрезке и дифференцируема во всех его внутренних точках, то внутри этого отрезка найдётся хотя бы одна точка , что справедливо равенство:

.

Доказательство. Рассмотрим график функции .

Напишем уравнение хорды АВ как уравнение прямой, проходящей через две точки А (а ; f (a)) и В (в ; f (в)):

.

Отсюда .

Составим вспомогательную функцию F(x): .

Эта функция удовлетворяет всем условиям теоремы Ролля.

Действительно, она непрерывна на , т.к. на нем непрерывны функции f(x) и (x-a). Производная существует в интервале (а,в), т.к. в нем существует . На концах отрезка F(a)=F(в)=0. По теореме Ролля внутри отрезке найдется такая точка Х=С, в которой :

. Отсюда .

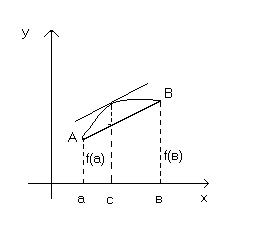
Геометрически теорема Лагранжа означает следующее:

Как видно из рисунка, отношение представляет собой угловой коэффициент хорды АВ, соединяющие концы дуги. Т.к. есть угловой коэффициент касательной, то теорема Лагранжа утверждает, что на графике функции найдется хотя бы одна точка, в которой касательная к графику параллельна хорде соединяющей концы дуги.

Формула называется формулой Лагранжа или формулой конечных приращений. Эта формула означает, что приращение дифференцируемой функции на отрезке равно длине отрезка (т.е. приращению аргумента ), умноженной на значение производной от этой функции в некоторой внутренней точке отрезка.

Теорема Коши. Если функции и  непрерывны на отрезке и дифференцируемы во всех его внутренних точках, причем  , то внутри этого отрезка найдется такая точка С, что справедливо равенство: .

Доказательство. Рассмотрим вспомогательную функцию

(х)- (а)).

Эта функция дифференцируема во всех точках интервала (а,в) и на его концах обращается в нуль: F(a)=F(в)=0.

Следовательно, по теореме Ролля, существует точка такая, что : . Отсюда . Это равенство называется формулой Коши.

Замечание 1. Из условия теоремы следует, что , т.к. в противном случае по теореме Ролля нашлась бы такая точка , что . Но это противоречит условию теоремы, согласно которому для всех .

Замечание 2. Теорема Лагранжа является частным случаем теоремы Коши, если положить (х)=х.