Замечательные пределы

1. .

Из него следуют следующие эквивалентности :

При . ,

2. или .

Отсюда следует, что , т.е. при

3. , т.е. при

Теорема

Если функции - бесконечно малые при , а функции , бесконечно малые, эквивалентные им соответственно, то

.

Примеры раскрытия неопределенностей

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8.

Непрерывные функции

Определение. Функция называется непрерывной в точке , если:

1. функция определена в точке и в некоторой окрестности, содержащей эту точку;

2. функция имеет предел при , причем .

Пример. .

Определение. Пределы и называются односторонними,

и соответственно , пределом справа и пределом слева.

Определение. Пусть определена в точке . Если , то говорят, что функция непрерывна в точке справа. Если , то говорят, что функция непрерывна в точке слева.

Замечание: Непрерывность функции в точке равносильна непрерывности в этой точке одновременно справа и слева.

Пример. .

Определение. Функция называется непрерывной на сегменте , если она непрерывна во всех внутренних точках этого сегмента, а на концах сегмента непрерывна соответственно справа и слева.

Свойства непрерывных функций

1. Если функции и непрерывны в точке , то и их сумма и произведение также непрерывны в точке . Если, кроме того, то функция непрерывна в точке .

2. Если функция непрерывна в точке , а функция непрерывна в точке , то сложная функция непрерывна в точке .

3. Если функция непрерывна на сегменте , то она достигает на этом сегменте своего наибольшего и наименьшего значения.

Следствие. Если функция непрерывна на сегменте , то она ограничена на этом сегменте.

4. Если функция непрерывна на сегменте и на его концах принимает значения разных знаков, то внутри сегмента найдется по крайней мере одна точка, в которой функция равна нулю.

Точки разрыва функции

Существуют функции, у которых имеются особые точки, предел в которых при стремлении к ним аргумента справа или слева существует, но имеют различные: ; .

Пример:

Определение. Точка называется точкой разрыва функции , если она принадлежит области определения функции или ее границе и не является точкой непрерывности.

Определения.

Точка разрыва функции называется точкой разрыва первого рода, если существуют конечные односторонние пределы и .

Разрыв первого рода фактически определяет скачок функции.

Точка разрыва, не являющаяся точкой разрыва первого рода, называется точкой разрыва второго рода.

Точка , в которой , а значение функции в этой точке неопределено, называется точкой устранимого разрыва.

Примеры.

1. Рассмотрим функцию .

Эта функция определена во всех точках сегмента и ее значение при равно 0.

Однако, в точке функция имеет разрыв первого рода, так как , а .

2. Функция в точке 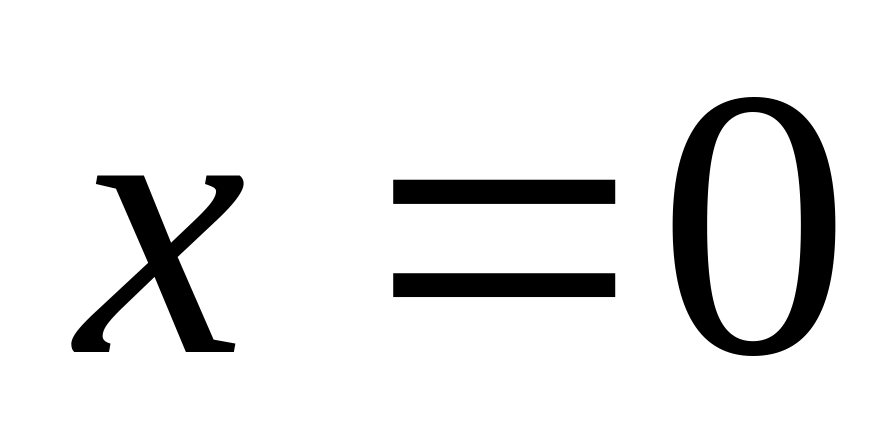имеет разрыв второго рода.

Функция не определена в точке . Точка является точкой разрыва первого рода, так как .

Если доопределить функцию в точке , полагая , то получим уже непрерывную функцию, т.е. мы устранили разрыв. Следовательно, точка устранимого разрыва.