МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ

Утверждена на заседании кафедры ИСС 26 апреля 2011 г.

Методические указания

по курсу

высшая математика

«Пределы и производные функции одной переменной

для бакалавров дневной формы обучения»

Ростов-на-Дону

2011

УДК 512.8 (08)

Методические указания по курсу высшая математика «Пределы и производные функции одной переменной» для бакалавров дневной формы обучения – Ростов н/Д: Рост. гос. строит. ун-т, 2011. – 40 c.

Изложен теоретический материал по пределам и производной функции.

Предназначена для бакалавров дневной формы обучения специальностей института ПГС.

Электронная версия находится в библиотеке, ауд. 224.

УДК 512.8 (08)

Составители:

канд. тех. наук, доц. Г.Я. Корабельников

асс. Е.А. Волкова

Рецензент:

д-р физ.-мат. наук, проф. А.А. Ляпин

Редактор Т.М. Климчук

Доп. план 2011 г., поз. 15

Подписано в печать 18.07.11. Формат 60х84/16.

Бумага белая. Ризограф. Уч.- изд. л. 2,0. Тираж 100 экз. Заказ 222

Редакционно-издательский центр

Ростовского государственного строительного университета

344022, Ростов - на - Дону, ул. Социалистическая, 162

 РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ

СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ, 2011

Последовательность, предел последовательности

Определение. Набор чисел, в котором каждому целочисленному значению номера ставится в однозначное соответствие значение , вычисляемое по некоторому закону, называется числовой последовательностью.

Примеры:

• члены арифметической прогрессии - ;

• члены геометрической прогрессии - .

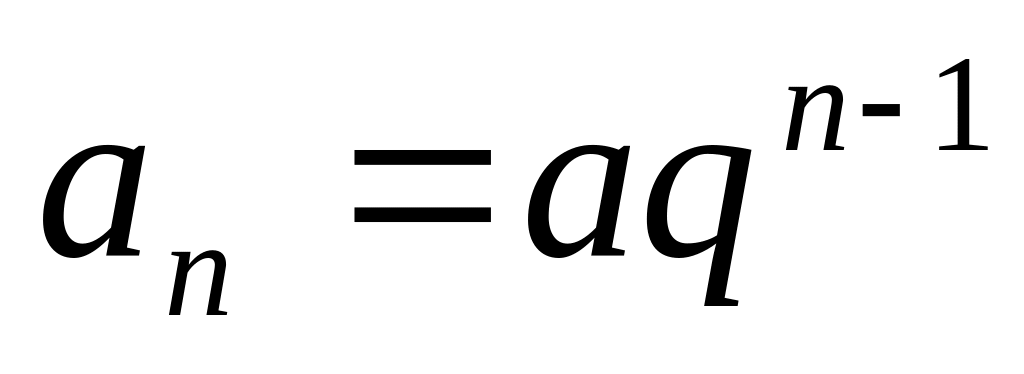Определение. Постоянное число называется пределом последовательности , если для любого сколь угодно малого числа существует такой номер , что все значения для удовлетворяют неравенству и обозначают

Величина называется сколь угодно малой, если она по абсолютной величине становится и остается меньшей сколь угодно малого наперед заданного числа , начиная с некоторого номера, т.е.

Лемма. Сумма любого конечного числа бесконечно малых величин есть также величина бесконечно малая.

Лемма. Произведение ограниченной величины на бесконечно малую величину есть величина бесконечно малая.

Определение. Переменная называется бесконечно большой, если она по абсолютной величине становится и остается большей любого, сколь угодно большого числа , начиная с некоторого номера для , т.е.

Если величина является бесконечно малой, то обратная для нее будет бесконечно большой. Аналогично, величина, обратная бесконечно большой, является бесконечно малой.

Свойства пределов

1. Если последовательности и имеют конечные пределы соответственно и , то их сумма (разность) также имеет предел, причем . Это свойство распространяется на любое конечное число слагаемых.

2. Если последовательности и имеют конечные пределы соответственно и , то их произведение также имеет предел, причем . Эта теорема может быть распространена на любое конечное число сомножителей.

3. Если последовательности и имеют конечные пределы соответственно и , причем , то их отношение также имеет предел, причем .

4. Если две последовательности равны ( ) и каждая из них имеет конечный предел, то и пределы их равны.

5. Если для двух переменных всегда выполняется неравенство , причем каждая из них имеет конечный предел и , то .

6. Если для переменных всегда выполняются неравенства , причем последовательности и имеют общий предел , то и .