16 Постулати спеціальної теорії відносності. Перетворення і додавання швидкостей в теорії відносності
Непосредственным следствием преобразований
Лоренца является релятивистское правило
сложения скоростей. Якщо певний об'єкт
має компоненти швидкості 
щодо
системи S і 
-
относительно S', то между ними существует
следующая связь:
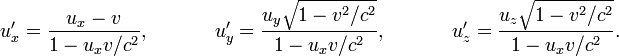
В этих соотношениях относительна скорость движения систем отсчёта v направлена вдоль оси x. Релятивістське складання швидкостей, як і перетворення Лоренца, при малих швидкостях ( ) Переходить в класичний закон додавання швидкостей.
Если объект движется со скоростью
света 
вздовж
осі x щодо системи S, то така ж швидкість
у нього буде і щодо S ': 
.
Це означає, що швидкість
является
инвариантной (одинаковой) во всех ИСО.
Нехай матеріальна точка рухається
у системі K' вздовж осі Ох зі
швидкістю , а
система рухається відносно K зі
сталою швидкістю 
,
напрямленою вздовж осі Ох (рис.1.49).
Тоді, використовуючи перетворення
Лоренца, отримуємо релятивістський
закон додавання швидкостей:
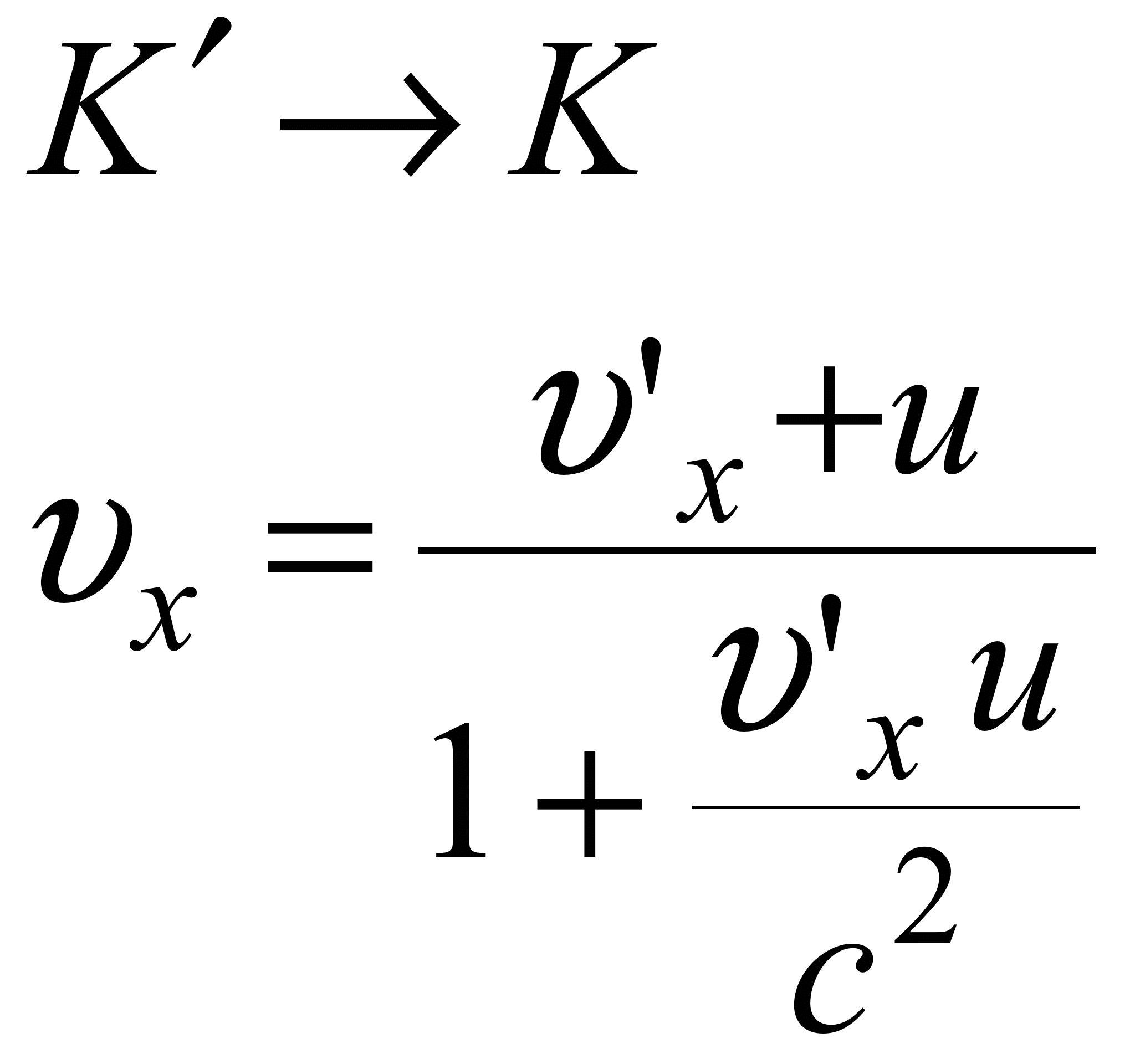
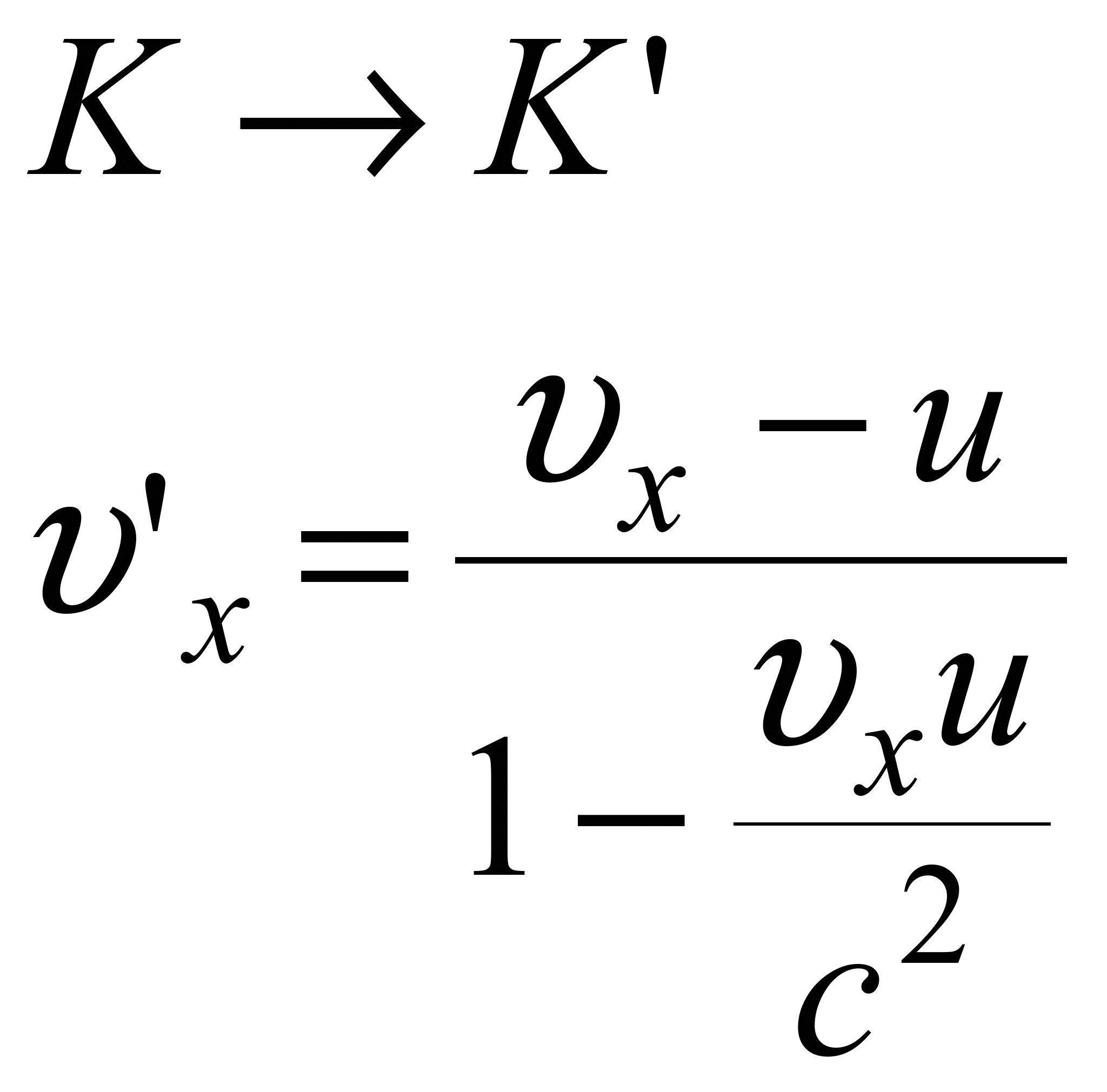Якщо
швидкості малі у порівнянні зі швидкістю
світла, то ці формули переходять у закон
додавання швидкостей у класичній
механіці Цей закон не протиріче і першому
постулату Ейнштейна, наприклад,
якщо u = c i ′x = c ,
то х = с,
отже, швидкість світла с є
максимальною, яку неможливо перевищити.
1. Знайдемо зв’язок між швидкістю
частинки
,
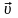що виміряна в системі відліку
,
та швидкістю тієї самої частинки
,
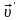що виміряна в системі відліку
.
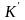Вважаємо, що система
рухається зі швидкістю
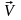відносно нерухомої системи
(див. рис. 43.1).
Компоненти швидкості частинки в системі визначаються виразами
,
,
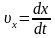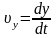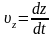. (43.1)
У системі компоненти швидкості тієї ж частинки дорівнюють
,
,
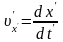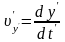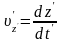. (43.2)
Знайдемо формули, що позв'язують нештриховані компоненти швидкості зі штрихованими. Для цього скористуємося перетвореннями Лоренца. Із цих формул отримуємо, що
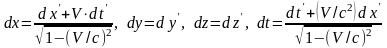. (43.3)
Розділивши перше із цих рівностей на четверте, прийдемо до співвідношення
,
яке з урахуванням (43.1) і (43.2) можна подати у вигляді
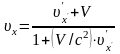. (43.4)
Розділивши друге й третє з рівностей (43.3) на четверте, отримаємо ще два співвідношення:
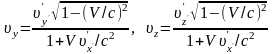. (43.5)
Формули (43.4) та (43.5) і розв’язують поставлене завдання. Вони отримали назву формули перетворення або додавання швидкостей в СТВ.
За формулами (43.4) і (43.5) здійснюється перетворення швидкостей при переході від системи до системи . Використавши аналогічно як і вище перетворення Лоренца, легко одержати формули
,
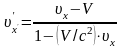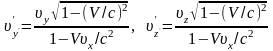, (43.6)
за якими здійснюється перетворення
швидкостей при переході від системи
до системи
.
Формули (43.6) відрізняються від формул
(43.4) і (43.5), як і слід було сподіватися,
тільки знаком перед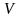 
.
Формули (43.6) також називаються формулами
перетворення або додавання швидкостей
в СТВ.
2. Проведемо дослідження формул додавання швидкостей в СТВ у граничних випадках.
Розглянемо випадок, коли
.
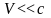У цій ситуації вираз
і ним можна в формулах (43.4)–(43.6) знехтувати.
У результаті отримуємо, наприклад, з
(43.4) та (43.5)
,
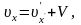
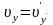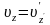
формули додавання швидкостей, за допомогою яких перетворюються швидкості в ньютонівській механіці. Таким чином, коли формули додавання швидкостей у СТВ переходять у формули додавання швидкостей ньютонівської механіки.
Розглянемо випадок, коли частинка
рухається паралельно осям
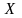і
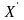в напрямку швидкості
(див. рис. 42.1). Тоді
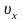збігається з модулем швидкості частинки
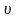в системі
,
a
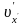– з модулем швидкості
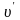в системі
,
і формула (43.4) має вигляд
. (43.7)
Швидкості
,
і
паралельні й направлені в одну й ту саму
сторону. Отже, формула (43.7) виражає закон
додавання швидкостей. Якщо
,
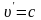то
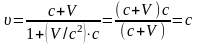. (43.8)
Таким чином, формула додавання швидкостей узгоджується с другим постулатом СТВ.