15. Постулати спеціальної теорії відносності. Перетворення Лоренца та висновки з них.

Спеціальна теорія відносності (СТВ) — фізична теорія, опублікована Альбертом Ейнштейном 1905 року. Вона фактично замінює класичну механіку Ньютона, яка на той час була несумісною з рівняннями Максвелла з теорії електромагнетизму.

Спеціальна теорія відносності не поширює дію своїх принципів на гравітаційні сили, тому в 1916 році Ейнштейн опублікував нову —загальну теорію відносності, яка пояснювала природу гравітації. В основу спеціальної теорії відносності (СТВ) А.Ейнштейном покладено два постулати:

* Перший постулат СТВ (принцип відносності): усі закони природи однакові у всіх інерціальних системах відліку. Цей постулат є поширенням принципу відносності Галілея на усі фізичні явища.

* Другий постулат СТВ (принцип інваріантності швидкості світла): швидкість світла у вакуумі однакова у всіх інерціальних системах відліку і не залежить від швидкостей руху як джерел, так і приймачів світла.

Перетворення Лоренца можуть бути отримані абстрактно, з групових міркувань (в цьому випадку вони виходять з невизначеним   ), Як узагальнення перетворень Галілея (що було пророблено Пуанкаре - см. нижче). Проте вперше вони були отримані як перетворення, щодо яких коваріантного рівняння Максвелла (тобто по суті - які не змінюють виду законів електродинаміки і оптики при переході до іншої системи відліку). Можуть також бути отримані з припущення лінійності перетворень і постулату однаковості швидкості світла у всіх системах відліку (що є спрощеною формулюванням вимоги ковариантности електродинаміки щодо шуканих перетворень, і поширенням принципу рівноправності інерційних систем відліку - принципу відносності - на електродинаміку), як це робиться в спеціальної теорії відносності (СТО) (при цьому   в перетвореннях Лоренца виходить певним і збігається зі швидкістю світла).

Треба зауважити, що якщо не обмежувати клас перетворень координат лінійними, то перший закон Ньютона виконується не тільки для перетворень Лоренца, а для більш широкого класу дробно-лінійних перетворень (проте цей більш широкий клас перетворень - за винятком, звичайно, окремого випадку перетворень Лоренца - не зберігає метрику постійної).

1. Алгебраїчний висновок

На підставі декількох природних припущень (основним з яких є припущення про існування принципово максимальної швидкості поширення взаємодій) можна показати, що при зміні ІСО повинна зберігатися величина

 ,

звана інтервалом. З цієї теореми безпосередньо випливає загальний вигляд перетворень Лоренца ( див. нижче). Тут розглянемо лише окремий випадок. Для наочності при переході в ІСО   , Рухому із швидкістю   , Виберемо в вихідної системі   вісь   сонаправленностью з   , А осі   і   розташуємо перпендикулярно осі   . Просторові осі ІСО   в момент часу   виберемо сонаправленностью з осями ІСО   . При такому перетворенні

Ми будемо шукати лінійні перетворення Лоренца, так як при нескінченно малих перетвореннях координат диференціали нових координат лінійно залежать від диференціалів старих координат, а в силу однорідності простору і часу коефіцієнти не можуть залежати від координат, тільки від взаємної орієнтації та швидкості ІСО.

Те, що поперечні координати не можуть змінюватися, ясно з міркувань ізотропності простору. Дійсно, величина   не може змінюватися і при цьому не залежати від   (Окрім як при обертанні навколо   , Яке ми виключаємо з розгляду), в чому легко переконатися підстановкою таких лінійних перетворень в вираз для інтервалу. Але якщо вона залежить від   , То точка з координатою   буде мати ненульову координату   , Що суперечить наявності симетрії обертання системи щодо   і изотропии простору. Аналогічно для   .

Найбільш загальний вигляд таких перетворень:

де   - Деякий параметр, званий швидкістю. Зворотні перетворення мають вигляд

Ясно, що точка, яка спочиває в ІСО   , Повинна буде рухатися в ІСО   зі швидкістю   . З іншого боку, якщо точка спочиває, то

Враховуючи, що при зміні ІСО не повинна змінюватися орієнтація простору, отримаємо, що

Отже, рівняння для швидкості однозначно розв'язні:

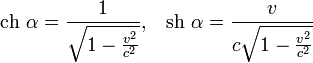
а перетворення Лоренца мають вигляд

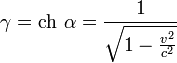
Параметр   називається лоренц-фактором.

Нехай координатні осі двох інерційних систем відліку S і S 'паралельні один одному, (t, x, y, z) - час і координати деякого події, що спостерігається щодо системи S, а (t ", x ', y', z ') - час і координати того ж події щодо системи S'. Якщо система S 'рухається рівномірно і прямолінійно зі швидкістю v відносно S, то справедливі перетворення Лоренца :

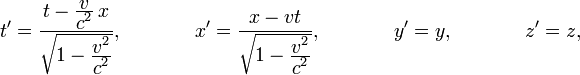
де c -Швидкість світла. При скоростях много меньше скорости света (   ) Перетворення Лоренца переходять в перетворення Галілея :

Подібний граничний перехід є відображенням принципа соответствия, согласно которому более общая теория (СТО) имеет своим предельным случаем менее общую теорию (в данном случае - класичну механіку).

Преобразования Лоренца можно записать в векторном виде [24], когда скорость систем отсчёта направлена в произвольном направлении (не обязательно вдоль оси x ):

де   - Фактор Лоренца,   і   - радиус-векторы события относительно систем S и S'.