Кривые второго порядка Эллипс

Эллипсом называется геометрическое место точек, сумма расстояний каждой из которых до двух точек и , называемых фокусами, есть величина постоянная и равная (рис. 5).

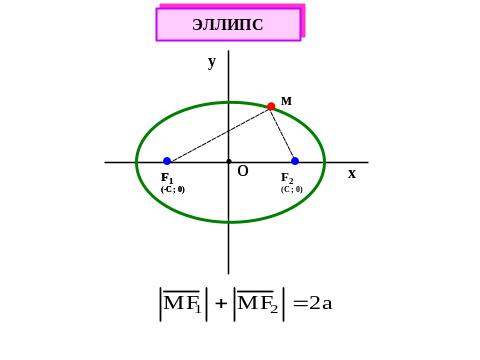
Рис. 5

Каноническое уравнение эллипса

.

Параметры и называются полуосями эллипса, большой и малой соответственно, если . Фокусы и находятся на оси Ох на расстоянии от центра.

Эксцентриситет эллипса есть отношение .

Расстояния точки эллипса от его фокусов определяются формулами , .

Примеры

1. Дано каноническое уравнение эллипса , найти его фокусы и эксцентриситет.

Из уравнения =4, =2, тогда и, следовательно, фокусы имеют следующие координаты , а эксцентриситет .

2. Написать каноническое уравнение эллипса, зная, что расстояние между фокусами равно 8, а малая полуось равна 3.

Из условия имеем , а . Тогда , отсюда .

Следовательно, каноническое уравнение эллипса имеет вид .

3. Написать каноническое уравнение эллипса, зная, что большая полуось равна 6, а эксцентриситет равен 0,5.

И условия . Тогда , отсюда . Используя формулу , найдем .

Следовательно, каноническое уравнение эллипса имеет вид .

Гипербола

Гиперболой называется геометрическое место точек, разность расстояний каждой из которых до двух точек и , называемых фокусами, есть величина постоянная и равная (рис. 6).

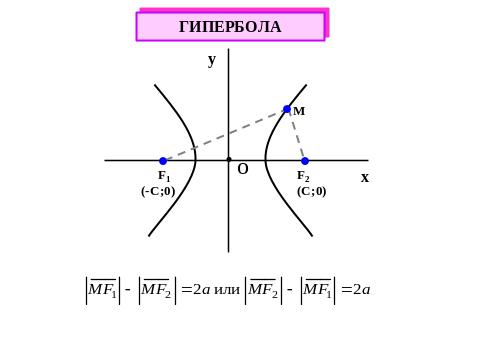
Рис. 6

Каноническое уравнение гиперболы .

Параметр называется вещественной полуосью, а - мнимой полуосью.

Эксцентриситет гиперболы есть отношение .

Расстояния точки от его фокусов определяются формулами: , .

Прямые называются асимптотами гиперболы.

Гиперболы и называются сопряженными.

Примеры

1. Дана гипербола . Найти ее асимптоты, фокусы, эксцентриситет.

Из условия , тогда получим уравнения асимптот . Найдем расстояние от центра до фокуса , а затем напишем координаты фокусов и вычислим эксцентриситет .

2. Написать каноническое уравнение гиперболы, зная, что расстояние между фокусами , а между вершинами

Из условия , тогда из формулы получим , теперь можно написать каноническое уравнение гиперболы .

3. Написать каноническое уравнение гиперболы, зная, что вещественная полуось , а эксцентриситет .

Используя формулу , найдем , тогда из формулы получим , теперь можно написать каноническое уравнение гиперболы .

Парабола

Параболой называется геометрическое место точек , одинаково удаленных от данной точки – фокуса и данной прямой – директрисы (рис. 7).

Каноническое уравнение параболы имеет два вида:

1. - парабола, симметричная относительно Ох;

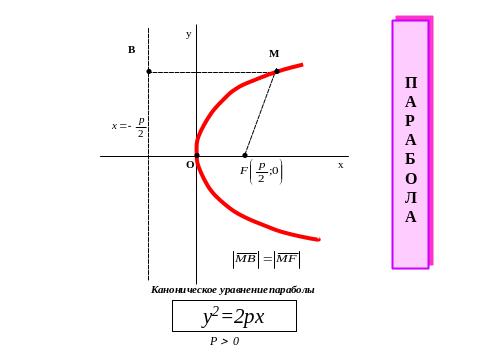
Рис. 7

2. - парабола, симметричная относительно Oу.

Парабола имеет фокус и директрису .

Парабола имеет фокус и директрису .

Примеры

1. Составить геометрическое место точек, одинаково удаленных от точки и прямой

Из условия , получаем , следовательно, это парабола, каноническое уравнение которой имеет вид или .

2. Написать уравнение параболы, проходящей через точку и и симметричной относительно оси Ох.

Каноническое уравнение параболы, симметричной относительно оси Ох и проходящей через начало координат, имеет вид . Подставим в это уравнение координата второй точки получим , тогда искомое уравнение имеет вид .