МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение высшего профессионального образования

«РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»

Утверждено на заседании кафедры ИСС 9 сентября 2009 г.

Методические указания

к практическим занятиям

по курсу «Высшая математика»

Раздел «Алгебра и аналитическая геометрия»

Часть 2

для студентов дневной формы обучения

института ПГС

Ростов-на-Дону

2010

УДК 512.8 (08)

Методические указания к практическим занятиям по курсу «Высшая математика». Раздел «Алгебра и аналитическая геометрия». Часть 2. – Ростов н/Д: Рост. гос. строит. ун-т, 2010.- 20 c.

Изложен теоретический и практический материал по линейной, векторной алгебре и элементам аналитической геометрии.

Предназначены для студентов дневной формы обучения специальностей института ПГС.

Составители:

канд. физ.-мат. наук, доц. А.Е. Богданов

канд. тех. наук, доц. Г.Я. Корабельников

ассист. Н.В. Неумержицкая.

Рецензент:

д-р физ.-мат. наук, проф. М.Г. Селезнев

Редактор Т.М. Климчук

Темплан 2010 г., поз. 106

Подписано в печать 16.03.10. Формат 60х84/16.

Бумага белая. Ризограф. Уч.-изд. л. 1,0. Тираж 100 экз. Заказ

Редакционно-издательский центр

Ростовского государственного строительного университета

344022, Ростов - на - Дону, ул. Социалистическая, 162

 РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ

СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ, 2010

Элементы аналитической геометрии Прямая линия на плоскости Уравнение прямой с угловым коэффициентом

, , где - угол наклона прямой к оси ОХ .

Если 1) , то прямая проходит через начало координат ;

2) , то прямая совпадает с осью ОХ .

Замечание. Уравнение описывает все прямые на плоскости за исключением прямых вида : .

Угол между двумя прямыми и .

. Угол между прямыми (рис. 1).

, Y

. Х

Рис. 1

Из полученной формулы следует:

1. Условие параллельности двух прямых; .

2. Условие перпендикулярности двух прямых; .

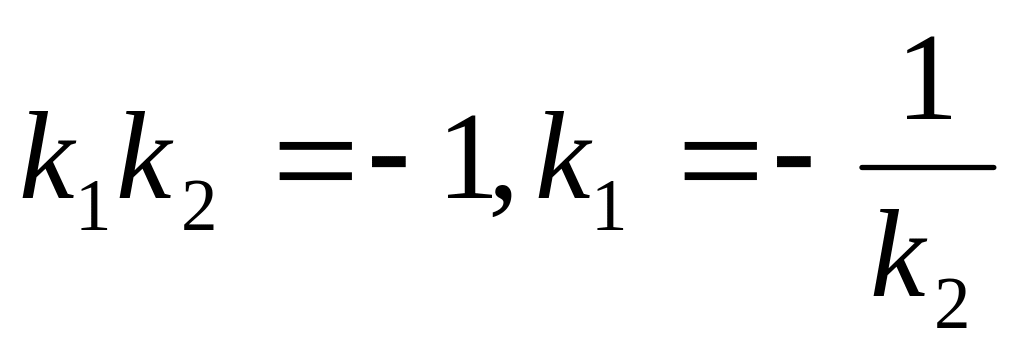Уравнение прямой, проходящей через заданную точку с заданным угловым коэффициентом

.

Уравнение пучка прямых

Рассмотрим уравнение .

Изменяя его угловой коэффициент, получим множество прямых, проходящих через точку , которое назовем пучком прямых, а рассматриваемое уравнение – уравнением пучка прямых.

Уравнение прямой , проходящей через две заданные точки

Уравнение прямой в отрезках на осях

(рис. 2).

Рис. 2

Примеры

1. Найти угол между двумя прямыми

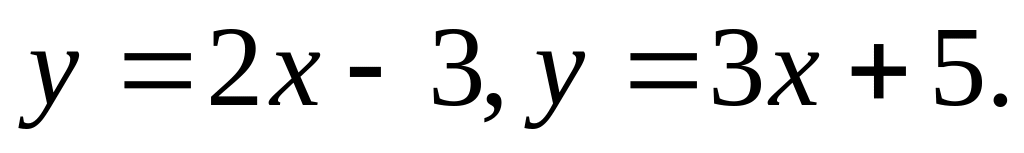
Из условия следует, что , тогда

, .

2. Написать уравнение прямой, проходящей через точку А

параллельно прямой .

Угловой коэффициент данной прямой , а из условия параллельности угловой коэффициент искомой прямой .Следовательно, уравнение параллельной прямой имеет вид Отсюда .

3. Написать уравнение прямой, проходящей через точку А

перпендикулярно прямой .

Угловой коэффициент данной прямой , а из условия перпендикулярности угловой коэффициент искомой прямой .

Следовательно, уравнение перпендикулярной прямой имеет вид

Отсюда .

4. Дана точка М( 1 ; 1 ). Провести через эту точку прямую под углом к прямой .

Воспользуемся уравнением пучка прямых , проходящих через точку (1,1) ,

. Теперь найдем угловой коэффициент искомой прямой, воспользовавшись формулой :

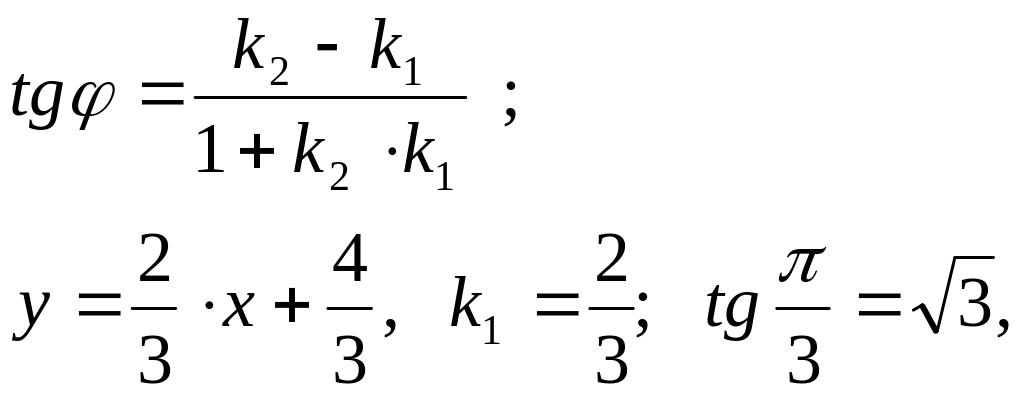
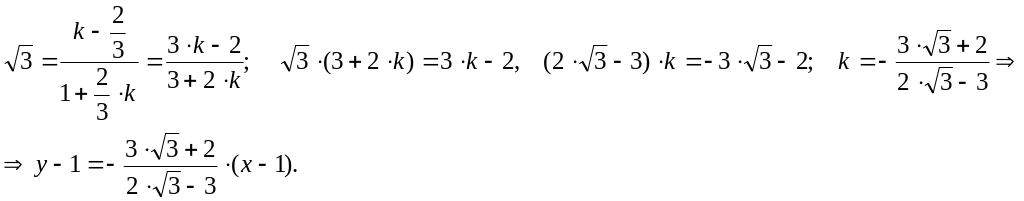
5. Дан треугольник с вершинами Найти уравнение высоты .

Найдем уравнение стороны как уравнение прямой, проходящей через две заданные точки и .

, отсюда .

Прямые и перпендикулярны, следовательно, угловой коэффициент прямой равен .

Теперь запишем уравнение прямой как уравнение прямой, проходящей через точку , с угловым коэффициентом

, отсюда

6. Дан треугольник с вершинами Найти уравнение медианы .

Точка D лежит на середине отрезка ВС, тогда ее координаты равны полусумме, соответствующих координат, точек В и С, т.е. .

Напишем уравнение прямой, проходящей через две точки A и B,

.Отсюда получаем искомое уравнение .

6. Прямая отсекает на оси ОХ отрезок длинной 5, а на оси ОY отрезок длинной 4.

Найти уравнение этой прямой.

Используя уравнение в отрезках на осях , получим . Отсюда получаем

.