Лекция 11 Многофазные смо и сети массового обслуживания Допущения для смо вида :

Распределение промежутков между заявками (вызовами) для первой СМО подчиняется экспоненциальному закону:

. (1)

Распределение длительности обслуживания вызовов для всех СМО подчиняется экспоненциальному закону:

(2)

Средние значения интервалов между вызовами и времени обслуживания определяется так:

, = . (3)

Условие стационарности каждой СМО:

. (4)

Сети массового обслуживания (СеМо)

Рассмотрим модель гипотетической сети, в которой установлено семь коммутаторов (К). Нас интересует процесс обмена информацией между К1 и К7. Между этими коммутаторами установлено три пути обмена пакетами, вероятность использования которых определяется величинами , и . Очевидно, сумма этих вероятностей равна единице.

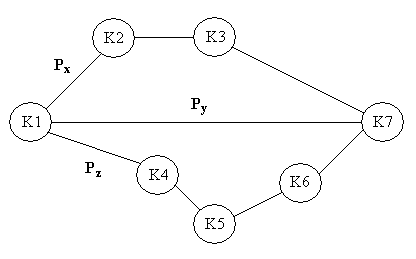
Допустим, что каждый коммутатор может быть представлен системой телетрафика с ожиданием. Интенсивность обработки пакета равна , а интенсивность входящего потока – .

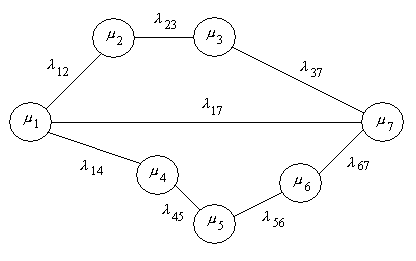
Допустим, что каждый коммутатор может быть представлен системой телетрафика вида . Тогда время пребывания пакета в коммутаторе определяется по такой формуле:

. (5)

Загрузка определяется отношением интенсивности входящего потока к интенсивности обслуживания. Например,

. (6)

Средняя задержка пакета на маршруте, выбираемом с вероятность , будет определяться так:

. (7)

Средняя задержка пакета в сети массового обслуживания ( ) может оцениваться с учетом вероятностей P_X, P_Y и P_Z:

= + + . (8)

Вычисление квантилей функции распределения длительности задержки пакетов существенно сложнее. Обычно для их расчета используют методы имитационного моделирования.

Многофазные системы массового обслуживания

В сети массового обслуживания можно выделить многофазные СМО, для которых осуществляется оценка показателей качества обслуживания трафика – задержки и/или потери заявок. Для произвольной структуры сети пример многофазной СМО можно представить такой совокупностью таких элементов:

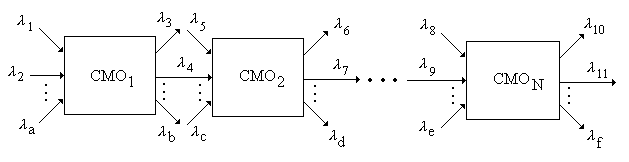
Для такой модели можно вычислить все интенсивности потоков заявок. Обычно для многофазных СМО определяются такие характеристики:

• вероятность потери заявок;

• среднее значение времени задержки заявок;

• функция распределения длительности задержки заявок.

Для алгоритма обслуживания заявок с потерями можно использовать приближенную формулу, если вероятность блокировки на каждой фазе весьма мала:

. (9)

Для среднего времени задержки заявок действует правило аддитивности математического ожидания:

= + + … + . (10)

Для функции распределения времени задержки заявок необходимо найти свертку таких же функций, определенных для каждой СМО. Преобразование Лапласа-Стилтьеса вычисляется проще:

. (11)

Сложные смо

1. Смо вида

Вероятности состояний ( ) определяются следующим образом:

, (12)

где – единственное решение уравнения

(13)

в области .

Распределение длительности ожидания для рассматриваемого класса СМО также определяется через переменную :

. (14)

Средняя длительность ожидания начала обслуживания рассчитывается так:

(15)

Для СМО вида уравнение (13), учитывая, что , принимает такой вид:

( . (16)

В уравнении (16) интересен только один корень в силу сформулированных ограничений – . Поэтому .