Лекция 9 смо с ожиданием

1. Смо вида

Распределение промежутков между заявками (вызовами) подчиняется экспоненциальному закону:

. (1)

Распределение длительности обслуживания вызовов подчиняется экспоненциальному закону:

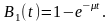(2)

Средние значения интервалов между вызовами и времени обслуживания определяется так:

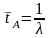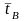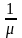, = . (3)

Условие стационарности СМО:

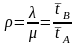
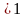. (4)

Вероятности состояний СМО:

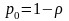
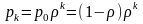. (5)

Среднее число заявок в СМО:

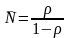. (6)

Дисперсия числа заявок в СМО:

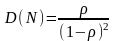. (7)

Среднее время ожидания заявок в очереди:

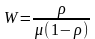. (8)

Среднее время пребывания заявок в системе:

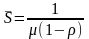. (9)

ФР длительности ожидания начала обслуживания:

. (10)

ФР длительности задержки заявок в СМО:

. (11)

Зависимости длины очереди и времени пребывания заявок в СМО от загрузки системы.

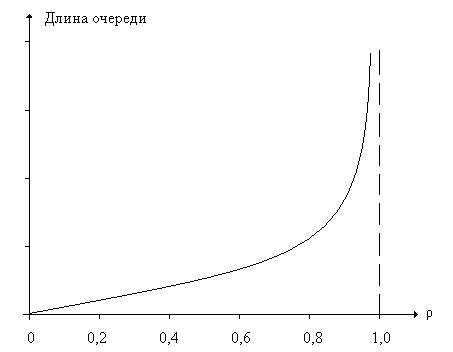
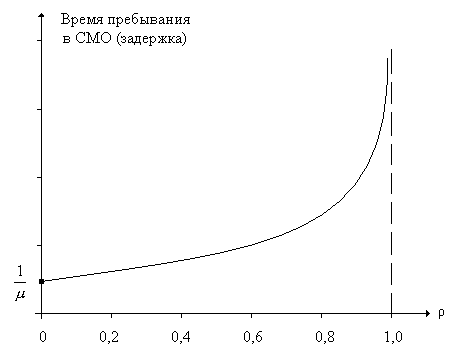
Преобразование Лапласа-Стилтьеса ФР интервалов между заявками, покидающими СМО:

. (12)

По двум моментам легко определяется коэффициент вариации:

. (13)

2. Смо вида

Состояние определяет наличие в СМО – в обслуживании и на ожидании – ровно заявок. Вероятность такого состояния СМО обозначается через . Можно показать, что СМО рассматриваемого вида справедливы такие соотношения:

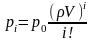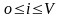
при

при 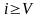(14)

.

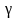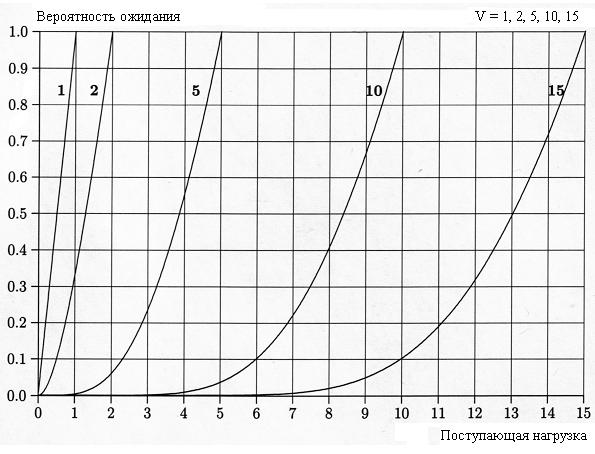
Ожидание (Waiting) обычно обозначат буквой "W". В некоторых старых монографиях встречается обозначение . Вероятность ожидания 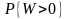определяется второй формулой Эрланга:

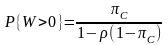, (15)

где – вероятность потери вызова, рассчитанная по первой формуле Эрланга для СМО без возможности ожидания.

Средняя длина очереди в СМО рассматриваемого вида определяется по такой формуле:

. (15)

Среднее время ожидания начала обслуживания 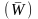рассчитывается по теореме Литтла:

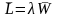. (17)

На графике показано поведение функции при различных величинах трафика и числа обслуживающих приборов.

ФР длительности ожидания:

. (18)

Для оценки эффективности дисциплины обслуживания с ожиданием определяется величина 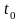, при которой :

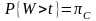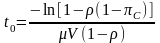. (19)

На графике показано влияние дисциплины обслуживания заявок на поведение плотности .

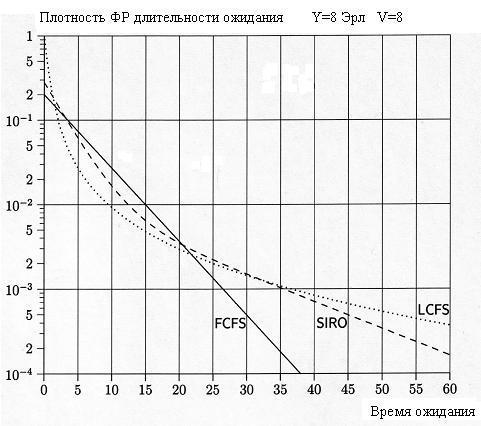
3. Смо вида

Среднее время ожидания заявок в очереди (формула Полячека-Хинчина):

. (20)

Среднее время пребывания заявок в системе (формула Полячека-Хинчина):

. (21)

Преобразование Лапласа-Стилтьеса ФР длительности ожидания начала обслуживания (уравнение Полячека-Хинчина):

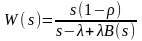. (22)

Преобразование Лапласа-Стилтьеса для ФР времени пребывания в СМО (уравнение Полячека-Хинчина):

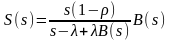. (23)

4. Смо вида

Вероятность потери заявок для рассматриваемой модели – определяется состоянием СМО , то есть . Для СМО с местами для ожидания эта вероятность определяется таким соотношением:

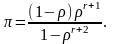(24)

Для СМО с неограниченным числом мест для ожидания в очереди вероятности состояний определяются следующим образом:

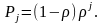(25)

Следовательно, вероятность того, что заявка застанет СМО в состоянии , будет определяться так:

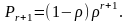(26)

Относительная ошибка в оценке вероятности потерь заявок – определяется простым соотношением:

(27)

На рисунке показана зависимость от при различных значениях . При достаточно малых вероятностях потерь (сравнительно больших значениях ) величины и быстро сближаются. Ошибка меньше для СМО с невысокой загрузкой. Кстати, – рекомендуемая величина загрузки для некоторых элементов сетей электросвязи. Если 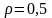, то значения ошибки при представляются приемлемыми для оценки исследуемых характеристик СМО. 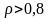Величины представляют интерес для режимов перегрузки отдельных элементов инфокоммуникационной сети. Для подобных задач использование величины вместо нельзя считать корректным из-за высоких значений ошибки .

Относительная ошибка при расчете

вероятности потерь заявок в двух видах СМО

Итак, при малой загрузке хорошей моделью системы можно считать СМО с неограниченным числом мест для ожидания.