Contents

Лекция 1 3

Лекция 2 18

1. Информация в сетях электросвязи 18

2. Алгоритмы обслуживания заявок 20

3 Классификация Кендалла-Башарина 23

Лекция 3 26

Качество обслуживания 26

1. Основные понятия 26

2. Качество обслуживания вызовов 30

3. Качество телефонной связи 34

4. Совершенствование качественных показателей 37

Лекция 4 38

Потоки заявок 38

Простейший поток 46

Лекция 5 46

Потоки заявок (продолжение) 46

1. Нестационарный и неординарный пуассоновские потоки 46

2. Потоки с простым последействием 47

3. Симметричный и примитивный потоки 48

4. Поток с повторными вызовами 49

5. Поток с ограниченным последействием. Поток Пальма 49

6. Просеивание потоков. Потоки Эрланга 49

7. Выходящие потоки 50

Лекция 5 51

Потоки заявок (продолжение) 51

1. Нестационарный и неординарный пуассоновские потоки 52

2. Потоки с простым последействием 53

3. Симметричный и примитивный потоки 53

4. Поток с повторными вызовами 54

5. Поток с ограниченным последействием. Поток Пальма 54

6. Просеивание потоков. Потоки Эрланга 55

7. Выходящие потоки 56

Лекция 7 56

Телефонная нагрузка 56

Лекция 8 63

СМО с потерями заявок (полнодоступный пучок) 63

Лекция 9 68

СМО с ожиданием 68

1. СМО вида 68

2. СМО вида 71

3. СМО вида 74

4. СМО вида 75

5. СМО вида 76

Лекция 10 77

1. Неполнодоступные системы 77

2. Многозвенные коммутационные системы 80

3. Повторные вызовы 81

Лекция 11 83

Многофазные СМО и сети массового обслуживания 83

Допущения для СМО вида : 83

Сети массового обслуживания (СеМО) 84

Многофазные системы массового обслуживания 85

Сложные СМО 86

Лекция 12 88

Аспекты измерения трафика 88

Лекция 13 96

Примеры задач, решаемых методами теории телетрафика 96

1. Определение пропускной способности АТС 96

2. Задачи, связанные с услугой "Прямая линия" 99

Современные задачи телетрафика 101

Лекция 14 102

Моделирование в теории телетрафика 102

Оператор Р₁₈ осуществляет проверку условия 109

Лекция 15 111

Фрактальные процессы и теория телетрафика 111

Лекция 1 Содержание курса лекций по теории телетрафика

Предмет курса "Теория телетрафика"

Математический аппарат теории телетрафика

Концепция качества обслуживания

Потоки вызовов

Телефонная нагрузка. Системы с потерями

Системы с ожиданием

Системы с приоритетами

Методы измерения телефонной нагрузки

Современные модели телетрафика

Итоги курса "Теория телетрафика"

Литература:

1. Л. Клейнрок. Теория массового обслуживания. – М.: Машиностроение, 1979.

2. Л. Клейнрок. Вычислительные системы с очередями. – М.: Мир, 1979.

3. Ю.Н. Корнышев, А.П. Пшеничников, А.Д. Харкевич. Теория телетрафика. – М.: Радио и Связь, 1996.

4. В.В. Крылов, С.С. Самохвалова. Теория телетрафика и ее приложения. – СПб.: BHV-Санкт-Петербург, 2005.

5. Г.П. Башарин. Лекции по математической теории телетрафика. – М.: РУДН, 2009.

6. С.Н. Степанов. Основы телетрафика мультисервисных сетей. – М.: Эко-Трендз, 2010.

7. А.Н. Соколов, Н.А. Соколов. Однолинейные системы массового обслуживания. – Учебное пособие, СПбГУТ, 2010

Конспекты лекций: http://nicksokolov.narod.ru

Предмет курса "Теория телетрафика"

Краткая история дисциплины "Теория телетрафика"

Базовые результаты теории массового обслуживания были сформулированы в начале XX века. Основоположником ее прикладной ветви – теории телетрафика – считается датский математик А.К. Эрланг, родившийся в 1878 и умерший в 1929 году. Именно на результаты А.К. Эрланга – как на базовые положения теории массового обслуживания – ссылаются специалисты, занимающиеся подобными исследованиями. В настоящее время теория массового обслуживания, помимо инфокоммуникационных систем, эффективно используется для решения задач торговли, транспорта и других сфер экономической деятельности.

Примеры задач, исследуемых методами теории телетрафика

Основные задачи, с которых началось развитие теории телетрафика, можно перечислить, используя классификацию Кендалла. Рассмотрим одну из самых простых СМО (систем массового обслуживания), обозначаемых в классификации Кендалла следующим образом:

. (1)

Символ в первой позиции классификации Кендалла определяет вид функции распределения длительности интервалов между моментами поступления соседних заявок – :

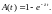(2)

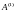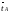Величина – интенсивность входящего потока заявок. Она измеряется числом заявок, поступающих в единицу времени. Математическое ожидание (среднее значение) длительности интервалов между моментами поступления соседних заявок (оно обычно обозначается символами или ) определяется следующим соотношением:

. (3)

Величина для любого вида функции может быть получена по известному правилу вычисления математического ожидания случайной величины. Символ во второй позиции классификации Кендалла определяет вид функции распределения длительности обслуживания заявок – :

(4)

Величина – интенсивность обслуживания заявок. Она измеряется числом заявок, которое СМО обслуживает в единицу времени. Математическое ожидание длительности обслуживания ( или ) определяется по такой формуле:

(5)

Символ " " в третьей позиции классификации Кендалла определяет численность обслуживающих приборов.

Модель широко используется в теории телетрафика. Например, пучок СЛ (соединительных линий) между коммутационными станциями в большинстве случаев изучают с помощью модели . Для пучка СЛ заявкой будет вызов, поступающий на вход соответствующей СМО. Длительностью обслуживания становится время занятия линии в пучке СЛ. Обслуживающим прибором следует считать набор из линий, образующих пучок СЛ.

Обычно пучок СЛ работает как СМО с потерями. Это означает, что при занятости всех линий поступивший вызов теряется. Вероятность потери вызова обозначим буквой . Для рассматриваемого примера практический интерес представляют четыре задачи:

• по известным величинам интенсивности входящего потока вызовов и интенсивности обслуживания найти такую емкость пучка СЛ (величину ), чтобы вероятность потерь не превышала заранее выбранный порог ;

• по известным величинам интенсивности входящего потока вызовов , интенсивности обслуживания и емкости пучка СЛ найти вероятность потери вызовов ;

• по известным величинам интенсивности входящего потока вызовов , емкости пучка СЛ и допустимой вероятности потерь вызовов найти допустимую величину интенсивности обслуживания ;

• по известным величинам интенсивности обслуживания , емкости пучка СЛ и допустимой вероятности потерь вызовов найти допустимую величину интенсивности входящего потока вызовов .

Если удастся составить уравнение с четырьмя неизвестными ( и ), то его всегда можно решить (хотя бы численными методами). Рассматриваемый пример – одна из важнейших практических задач эффективного развития сетей телефонной связи в начале XX века. Ее успешно решил А.К. Эрланг. Он вывел формулу, определяющую зависимость вероятности потерь от величин , и . Она получила название "Первая формула Эрланга".

Теперь усложним задачу. Рассмотрим цифровой тракт между коммутационными станциями мультисервисной сети. По этому тракту передаются пакеты, для обслуживания которых используется дисциплина с ожиданием. Из очереди пакеты извлекаются с учетом назначенных им приоритетов для обработки и передачи. Понятно, что исследование систем, описывающих процессы обмена пакетами в мультисервисной сети, заметно сложнее, чем анализ модели . К перечисленным выше четырем задачам, представляющим практический интерес, следует добавить такие проблемы:

• анализ длительности задержки пакетов в узлах мультисервисной сети;

• выбор оптимальных правил назначения приоритетов с учетом факторов, характерных для мультисервисной сети.

Сложность анализа систем телетрафика зависит от вида функций и , а также от алгоритма обслуживания заявок. Кроме того, сложность этого анализа определяется способом нормирования показателей качества обслуживания. Если показатель качества обслуживания нормируется только средним значением (математическим ожиданием), то анализ систем телетрафика обычно не сложен. Если нормируется параметр, для которого необходимо знать вид распределения случайной величины, то часто требуются сложные исследования.