48. Явление удара. Ударная сила и ударный импульс. Основное уравнение теории удара

49..Прямой удар тела о неподвижную поверхность. Коэффициент восстановле ния при ударе.

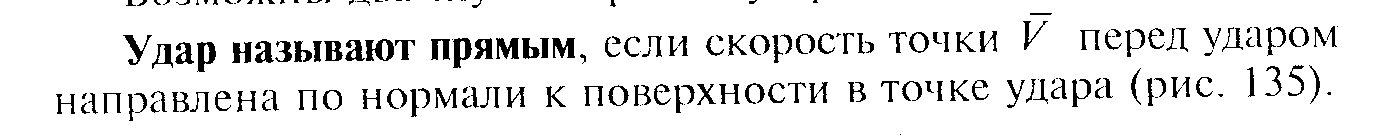
50. Косой удар тела о неподвижную поверхность.

Скорость тела до удара v направлена под углом падения α к общей нормали n тела и поверхности (рис. 1,б). После удара тело отскакивает от неподвижной поверхности со скоростью u под углом отражения β к общей нормали h.

Между скоростями u и v и между углами α и β имеет место соотношение:

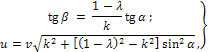
где λ - коэффициент мгновенного трения, определяемый экспериментально (часто полагают λ=0).

рис. 1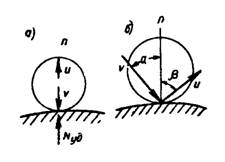

α – угол падения

β – угол отражения

51 Прямой центральный удар двух тел- Частные случаи.

Скорости тел v₁ и v₂ до удара направлены по их общей нормали, проходящей через их центры масс. Различают две фазы удара:

первая фаза: от момента соприкосновения тел до момента, когда все точки соударяющихся тел приобретут общую скорость u и оба тела получат максимальную деформацию. Скорость u в конце фазы:

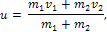
где m₁ - масса первого тела; m₂ - масса второго тела;

вторая фаза: с момента окончания первой фазы до того момента, когда тела под действием упругих сил частично восстановят свою форму, приобретут разные скорости u₁ и u₂ и разъединятся. Скорости тел после удара:

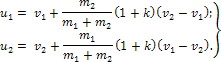
Полный ударный импульс, полученный каждым из тел при ударе:

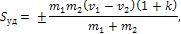
где знак минус берется для первого тела, а знак плюс для второго.

52. Потеря кинетической энергии при ударе. Теорема Карно.

КИНЕТИЧЕСКАЯ ЭНЕРГИЯ, ПОТЕРЯННАЯ ПРИ УДАРЕ. При ударе часть кинетической энергии ударяющихся тел ?T теряется, т. е. переходит в немеханические формы:

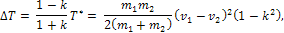
где Т* - кинетическая энергия потерянных скоростей v₁-u₁ и v₂-u₂:

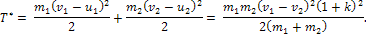
Частные случаи:

k=0,

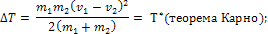
k=1, ?T=0 (потери энергии не происходит).

53. Удар по вращающемуся телу.

Удар по вращающемуся телу.

При исследовании удара по вращающемуся телу кроме теоремы об изменении количества движения приходится использовать и закон моментов. Относительно оси вращения его запишем так и, после интегрирования за время удара , или где и - угловые скорости тела в начале и в конце удара, - ударные силы.

Правую часть надо немного преобразовать. Найдем, сначала, интеграл момента ударной силы относительно неподвижной точки О:

.

При этом предполагалось, что за малое время удара τ радиус-вектор считался неизменным, постоянным.

Проектируя результат этого векторного равенства на ось вращения z, проходящую через точку О, получим , т.е. интеграл равен моменту вектора импульса ударной силы относительно оси вращения. Закон моментов в преобразованном виде запишется, теперь, так:

. (10)

В качестве примера рассмотрим удар вращающегося тела о неподвижную преграду.

Тело, вращаясь вокруг горизонтальной оси О, ударяется о преграду А (рис.114). Определим ударные импульсы сил, возникающих в подшипниках на оси, и

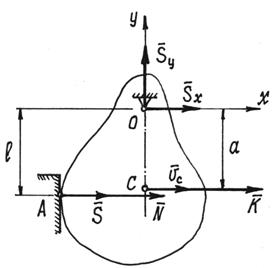Рис.114

 

По теореме об изменении количества движения в проекциях на оси х и у получим два уравнения:

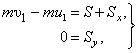
где скорости центра масс С в начале и конце удара Поэтому первое уравнение станет таким

Третье уравнение, по (10), получится в виде из которого находим

И, так как коэффициент восстановления

то (в нашем примере поэтому ударный импульс S > 0, то есть направлен так, как показано на рисунке).

Находим импульсы реакции оси:

Обязательно надо обратить внимание на то, что при ударные импульсы в подшипниках оси будут равны нулю.

Место, точка удара, расположенная на этом расстоянии от оси вращения, называется центром удара. При ударе по телу в этом месте ударные силы в подшипниках не возникают.

Кстати, заметим, что центр удара совпадает с точкой где приложены равнодействующая сил инерции и вектор количества движения.

Вспомним, что при ударе длинной палкой по неподвижному предмету, мы нередко испытывали рукой неприятный ударный импульс, как говорят – «отбивали руку».

Нетрудно найти в этом случае центр удара – место, которым следует ударить, чтобы не почувствовать это неприятное ощущение (рис.115).

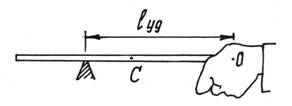
Рис.115

 

Так как (l – длина палки) и то

Следовательно, центр удара находится на расстоянии трети длины от конца палки.

Понятие центра удара учитывают при создании различных ударных механизмов и других конструкций, где встречаются ударные процессы.