42.Линейное сопротивление и диссипативная функция.
ДИССИПАТИВНАЯ ФУНКЦИЯ (функция рассеяния) - ф-ция, вводимая для учёта перехода энергии упорядоченного движения в энергию неупорядоченного движения, в конечном счёте - в тепловую, напр., для учёта влияния сил вязкого трения на движение механич. системы. Д. ф. характеризует степень убывания механич. энергии этой системы. Д. ф., делённая на абс. темп-ру, определяет скорость, с к-рой возрастает энтропия в системе (т. н. производство энтропии). Д. ф. имеет размерность мощности.
Д.
ф. может быть построена для механич.
систем, у к-рых скорости макроскопич.
движений настолько малы, что силы
сопротивления движению можно считать
линейно зависящими от скоростей. Если
положение такой системы определяется
обобщёнными координатами q1, q2, . . ., qS, то
для неё Д. ф. является квадратичной
формой обобщённых скоростей
:
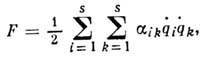
где
- размерные коэфф., зависящие в общем
случае от координат qi.
Величина F всегда положительна и численно
равна половине полной механич. энергии
E системы, рассеивающейся в единицу
времени:
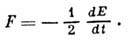
Зная
Д. ф., можно вычислить соответствующую
каждой координате qi
силу сопротивления
и составить дифференц. ур-ния движения
системы в лагранжевой форме:
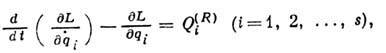
43…..
44. Вынужденные колебания системы без учета сопротивления
45. Явление резонанса.
Явление резонанса возникает при совпадаении частот вынужденных и свободных кол-ний точки p=k. Диф-ное ур-ние: . Частное решение:
х**= Вtcos(kt+d), B=—h/(2k), т.е. общее решение диф-ного ур-ния: х = C1coskt + C2sinkt — —h/(2k)tcos(kt+d). Ур-ние показывает, что амплитуда вынужденных колебаний при резонансе возрастает пропорционально времени. Период
Т=2p/k, фаза вынужденных колебаний отстает от фазы возмущающей силы на p/2.
46. Влияние линейного сопротивления на вынужденные колебания.
1) Линейное сопротивление не влияет на частоту вынужденных колебаний, которая совпадает с частотой возмущающей силы.
2) Вынужденные колебания при линейном сопротивлении не зависят от начальных условий, так же как они не зависят от них при отсутствии сопротивления.
3) Амплитуда вынужденных колебаний стремится к нулю быстрее при линейном сопротивлении с увеличением относительной частоты возмущающей силы, чем при отсутствии сопротивления.
4) Другая важная особенность влияния линейного сопротивления на вынужденные колебания связана с явлением резонанса. В случае резонанса при линейном сопротивлении амплитуда вынужденных колебаний не возрастает пропорционально времени, как при отсутствии сопротивления, а остается постоянной величиной. Достаточно как угодно малого сопротивления, чтобы амплитуда вынужденных колебаний при резонансе была постоянной, хотя, возможно, и достаточно большой, но не переменной, возрастающей с течением времени.
47. Исследование вынужденных колебаний. Коэффициент расстройки, коэффициент динамичности. Амплитудно-частотная и фаза-частотная характеристики системы.
Коэффициентом динамичности в теории колебаний называют безразмерную скалярную физическую величину, определяемую следующим выражением:
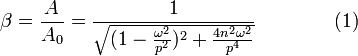
где
А — амплитуда
А_0 — равновесная амплитуда представляющая собой статическую деформацию упругой связи под действием максимальной силы P_0
ω — частота возмущения
p — собственная частота колебаний
n — коэффициент, характеризующий силы вязкого трения
Фазо-частотная характеристика (ФЧХ) — частотная зависимость разности фаз между выходным и входным сигналами.
Амплитудно-частотная характеристика (АЧХ) — функция, показывающая зависимость модуля некоторой комплекснозначной функции от частоты.