31. Приведение сил инерции точек мс и тв тела к простейшему виду. Частные случаи приведения.

К системе сил инерции точек твердого тела можно применить метод Пуансо – метод приведения сил к некоторому центру, рассмотренный в статике. В динамике за центр приведения сил инерции выбирают обычно центр масс тела С. Тогда в результате приведения получится сила Ф*, равная главному вектору сил инерции точек тела, и пара сил с моментом М*.

Главный вектор сил инерции точек твердого тела при любом ее движении: Ф* = –mwc.

Остается определить главный момент сил инерции точек тела относительно центра масс.

Рассмотрим некоторые случаи движения твердого тела.

1) Поступательное движение. Ф = Ф* = –mwc.

2. Вращение твердого тела, имеющего плоскость материальной симметрии, вокруг неподвижной оси, перпендикулярной к этой плоскости

3. Вращение твердого тела, имеющего плоскость материальной симметрии, вокруг центральной оси, перпендикулярной к этой плоскости.

В этом случае ось вращения тела является главной центральной осью инерции тела, так

как она проходит через центр масс тел, перпендикулярно к плоскости симметрии

Ф* = –JC2ε.

4. Плоское движение твердого тела, имеющего плоскость материальной симметрии.

32.Динамические реакции при вращении тв тела вокруг неподвижной оси.

При движении несвободного твердого тела реакции связей, действующие на это тело, складываются из статических и добавочных динамических составляющих.

R^e=R^eст+R^eдин, где R^eст − главный вектор статических реакций, R^eдин − главный вектор динамических реакций.

Статические реакции определяются из уравнений статики, а динамические обусловлены движением тела и определяются только силами инерции.

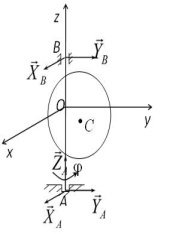
Динамические реакции подшипников при вращении твердого тела вокруг неподвижной оси с учетом принципа д’Аламбера можно определить из следующей системы уравнений

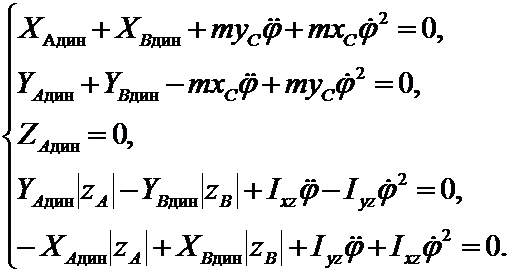
33. Связи и их уравнения. Классификация связей.

По виду своих ур-й связи разделяют на удерживающие и неудерживающие, стационарные и нестационарные. Связь назыв удерживающей или двусторонней если ее ур-е имеет вид строгого равенства. ( матем маятник в случае закрепл при пом стержня x²+y²=l²) l –длина стержня, х,у – корд точки. 2 мат точки соед между собой невес жестким стержнем : (x1-x2)²+(y1-y2)²+(z1-z2)²=l²

Если ур-е связи имеет вид равенства-неравенства, то связь – одностор (неудерж). Матем маятник закрепл при пом нити x²+y²≤ l² .Катящееся колесо опорной плоскостью yc-R≥0.

Связь (удерж или неуд) назыв стационарной если в ее уравнение время t не входит явным образом, в противном случае связь – нестационарная. Идеальная связь – если возможная работа реакции связи равна 0.

34. .Возможные перемещения. Число степеней свободы системы. Виртуальная работа. Идеальные связи

Возможные (виртуальные) перемещения системы (ds, dj) — любая совокупность бесконечно малых перемещений точек системы, допускаемых в данный момент наложенными на систему связями. Возможные перемещения рассматривают как величины первого порядка малости, пренебрегая при этом величинами высших порядков малости. Т.е. криволинейные перемещения точек заменяют прямолинейными отрезками, отложенными по касательным к их траекториям.

Число независимых между собою возможных перемещений системы называется числом степеней свободы этой системы. Например. шар на плоскости может перемещаться в любом направлении, но любое его возможное перемещение может быть получено как геометрическая сумма двух перемещений вдоль двух взаимно перпендикулярных осей. Свободное твердое тело имеет 6 степеней свободы.

Возможная (виртуальная) работа dА — элементарная работа, которую, действующая на матер.точку сила могла бы совершить на возможном перемещении этой точки.

Связи являются идеальными, если сумма элементарных работ реакций этих связей при любом возможном перемещении системы равна нулю, т.е. SdАr=0.