Пристрої множення і ділення, їхні різновиди. Особливості побудови.
Обчислюючі
пристрої, які служать для відтворення
обчислень виду
та наз. пристроями множення і ділення.
Відповідну операцію необхідно виконувати
з зазанченою точністю, в заданих
діапазонах ампілтуд і частот вхідних
сигналів. В залежності від знаків вхідних
змінних розрізняють одно-, дво- і
чотирьохквадратні прситрої. В
одноквадратних пристроях використовують
вхідні напруги одного знаку, в двоквадратних
– змінюється знак однієї, а в
чотирьохквадратних – обох змінних.
При побудові схем прсистроїв такого типу використовують компаратори.
Множення і ділення може проводитися на основі різних принципів. За способом виконання математичної опреції пристрою множення і ділення поділяються на два класи: 1) пристрої прямої дії, коли мат. операції виконуються безпосередньо на основі фізичних процесів, які протікають в електричних колах; 2) пристрої непрямої дії, коли реалізуються різні мат. співвідношення, результатом яких є множення чи ділення заданих велични.
Пристрої множення і ділення прямої дії:
- пристрої розімкнутого типу, в яких коефіцієнт передачі керованого елемента лінійно залежить від одного із співмножників. Точність роботи визначається якістю виготовлення елемента із керованим коефіцієнтом передачі. До таких елементів висуваються високі вимоги по лінійності, стабільності і динамічному діапазоеу.
- пристрої замкненого типу, в яких коефіцієнт передачі керованого елемента змінюється автоматично в електричному колі від’ємнорго зворотнього зв’язку і тому виогои до елементів значно знижуються.
Інтегратори на оп. Принципи побудови і функціонування. Приклади використання.
В активних RC-схемах часто застосовують так званий інтегратор Міллера (мал.11.1), що містить операційний підсилювач (ОП), конденсатор і резистор.
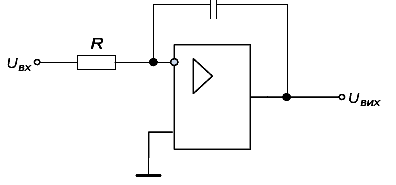
Мал. 11.1. Активний інтегратор на RC елементах.
Така_схема_виконує_функцію_інтегрування:
Якщо в інтеграторі Міллера замінити резистор R відповідним блоком з перемикаючими конденсаторами, то отримаємо активний інтегратор на перемикаючих конденсаторах (мал.11.2).
Мал.11.2. Інтегратор на ПК.
Принципи побудови пристроїв, що виконують математичні операції логарифмування і потенціювання.
Логари́фм
числа «b» по основанию «a» вычисляется,
как показатель степени, в которую
необходимо возвести основание «a», чтобы
получить число «b». Обозначение:
Из
определения следует,
что
записи и равносильны, но выполняют
противоположные операции (логарифмирования
и потенцирования).
Логарифмирование — нахождение значения логарифма. Для алгебраических выражений логарифмирование может подразумевать выражение логарифма выражения через логарифмы составных частей (в пределе - чисел), входящих в выражение.
Потенцирование — нахождение исходного значения или выражения, от которого получено значение в результате логарифмирования.
Например
Програмування задач на аом. Мова програмування. Елементи мови, їх характеристики.
АВМ иначе называют моделирующими установками или электронными моделями.
В развитии современного естествознания метод моделирования имеет большое значение. Моделирование, как метод научного исследования, появилось в связи с необходимостью решать такие задачи, которые по каким-либо причинам, например, в силу дороговизны, опасности или невозможности прямого эксперимента не могли быть решены непосредственно.
Различают физическое и математическое моделирование.
Сущность физического моделирования заключается в том, что вместо сложного процесса определенной физической природы исследуют этот же процесс, но в других масштабах (например, модели самолетов, кораблей). Физическое моделирование базируется на физическом подобии явлений в оригинале и модели, а, в ряде случаев, и их геометрическом подобии.
Сущность математического моделирования заключается в том, что исследование сложного процесса одной физической природы заменяется исследованием процесса другой физической природы.
В основе обоих видов моделирования лежит математическое подобие между оригиналом и моделью. Частным случаем является физическое подобие и физическая аналогия, т.е., физическое моделирование есть частный случай математического.
Методика математического моделирования сводится к следующем этапам:
а) Составление уравнения (или системы уравнений) для моделируемого процесса:
F (y, xj, qi, t) = 0
б) Выбор известной или создание новой математической модели, знаковое описание которой аналогично описанию оригинала
FM (yM, xMj, qMi, tM) = 0
Уравнение модели обычно называют машинным уравнением.
в) Обеспечение подобия уравнений за счет соответствующего выбора определения масштабов моделей
My = yM / y; Mx = xM / x; Mt = tM / t = t / t
и расчета коэффициентов машинного уравнения;
г) Решение на модели машинного уравнения FM = 0.