61. Структурні міри інформації. Статична міра інформації, поняття ентропії.

1. Геометрическая мера.Определяют количество информации по числу информационных элементов (квантов), занимающих определенную область информационного поля.

Информационная емкость – максимальное количество квантов, размещаемых в заданных структурных габаритах.

Например, для трехмерного информационного поля, имеющего по осям координат протяженности X, Y, Z и имеющего шаги квантования по осям DX,DY,DZ информационная емкость будет определяться формулой:

2. Комбинаторная мера.

Количество информации измеряется числом комбинаций информационных элементов в информационной системе.

Для текстовых сообщений наиболее применимый способ комбинирования - размещение с повторением. Наибольшее число комбинаций для этого способа: L=mn

Число размещений из m элементов по n является степенью => зависимость количества информации L от длинны сообщения нелинейна.

Если измеряем обобщенное количество информации нескольких источников сообщений, то общее количество информации определяется как произведения информативности отдельных источников:

3. Логарифмическая мера.

Автором этой меры является Хартли. Выделение логарифма позволяет избавиться от главного недостатка комбинаторной меры - нелинейной зависимости количества информации от длины сообщения.

Логарифмическая мера определяется по формуле: I=Loga(L)

Основание логарифма (a) определяет единицу измерения количества информации, основание может быть любое, например:

а=10 - единица измерения дит;

а=е - единица измерения нит;

а=2 - единица измерения бит.

1 бит информации содержится в ответе на вопрос, допускающий 2 равновероятных ответа - да или нет. В ответе да/нет один вид информации.

Ентропія є мірою невизначеності випадкової величини. Зазвичай, в якості інформаційної ентропії використовують ентропію Шеннона.

Ентропія Шеннона визначає абсолютну межу найкращого стиснення даних без втрат.

61. Властивості безумовної ентропії.

Об'єднання - сукупність двох і більше ансамблів дискретних, випадкових подій. З об'єднанням пов'язані поняття умовної, безумовної, спільної та взаємної ентропії.

1. Безумовна ентропія - середня кількість інформації, що припадає на один символ (рис. 1). Якщо Х - передається, а У - прийняте повідомлення, то можна записати наступні співвідношення:

H (X) = H (X / Y) + H (X × Y),

H (Y) = H (Y / X) + H (X × Y).

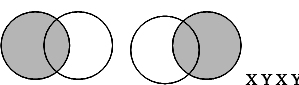Рис. 1. Безумовна ентропія

61. Умовна ентропія, властивості умовної ентропії.

Умовна ентропія - кількість інформації про джерело, коли відомо, що приймається Y, або міра кількості інформації в приймачі коли відомо, що передається X (рис. 2).

H (X / Y) = H (X)-H (X? × Y)

H (Y / X) = H (Y)-H (X? × Y).

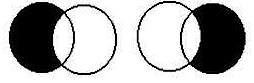X Y X Y Рис. 2. Умовна ентропія

61. Ентропія й інформація, властивості інформації.

Базисным понятием всей теории информации является понятие энтропии. Энтропия – мера неопределенности некоторой ситуации. Можно также назвать ее мерой рассеяния и в этом смысле она подобна дисперсии. Но если дисперсия является адекватной мерой рассеяния лишь для специальных распределений вероятностей случайных величин (а именно – для двухмоментных распределений, в частности, для гауссова распределения), то энтропия не зависит от типа распределения. С другой стороны, энтропия вводится так, чтобы обладать, кроме универсальности и другими желательными свойствами. Так, мера неопределенности была аддитивной: f(nm)=f(n)+f(m). Именно такая удобная мера неопределенности была введена К. Шенноном:

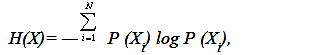где Х – дискретная случайная величина с диапазоном изменчивости N, P(Xi) – вероятность i – го уровня X.