19. Формула Пуассона умови її використання.

Ця формула використовується в схемі Бернуллі, якщо n дуже велике ( ), а p фбо q дуже мале( ), то використовують формулу Пуассона.

Де , е- стала(е=2.7), а

20. Означення випадкової величини, неперервної та дискретної випадкових величин.

ВВ наз. Таку величину, яка внаслідок випробування прийняти лише одне числове значення заздалегідь невідоме і обумовлене випадковими причинами(Х;У;Z),а їх значення . ВВ ділиться на два класи Дискретні випадкові величини та неперервні випадкові величини.

ДВВ- це ВВ можливими значеннями яких є окремі ізольовані числа з деякими ймовірностями.

НВВ- це ВВ, яка може приймати значення з деякого скінченного бо нескінченного проміжку.

21. Закон розподілу випадкової величини.

Для задання ВВ потрібно задати не тільки її значення , а і для кожного значення ВВ вказати його ймовірність.

Закони розподілу ВВ наз. Таке співвідношення, яке встановлює зв'язок між значенням ВВ і відповідної їм ймовірності.

22. Інтегральна функція розподілу випадкової величини:означення, властивості.

Інтегральною ф-ією розподілу(або ф-ією розподілу ймовірності) наз ф-ія F(x), яка визначає для кожного значення х Р того, що ВВ Х набуде значення менше, ніж x.

F(х)=Р(Х<x)

Властивості:

0 (за означенням F=P)F(x) являється неспадною (зростаючою)ф-ією, а саме якщо

Ймовірність того, що ВВ Х прийме значення з інтервала від а до b обчислюється за формулою

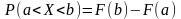
Якщо ВВХ є неперервною, то Р того, що вона набере конкретного значення дорівнює 0 Р(Х= )=0, тому ймовірність, що

Якщо НВВ Х належить проміжку від а до b, то НВВ Х є [a;b],то F(x)=0, при х ;F(x)=1, при х<b.

23.Диференціальна функція розподілу(щільність розподілу) випадкової величини:означення, властивості.

Диференціальною функція розподілу(щільністю ймовірностей) НВВ Х наз. Похідну першого порядку від інтегральної ф-ії розподілу.

f(x)=F(x)

Властивості:

f(x) , так як являється похідною від зростаючої ф-ії. Графік f(x) лежить лише в верхній півплощині.

Р попадання НВВ Х є [a,b] обчисл. За формулою

Умова нормування НВВ :

А)якщо Х є(- ), то (подія являється достовірною);

Б)Х є (a;b), то

24.Математичне сподівання випадкової величини:означення, властивості

Математичне сподівання ДВВ Х – це число,яке дорівнює сумі добутків усіх можливих значень ВВ на відповідні їм ймовірності.

М(Х)= - для ДВВ

Матем. Сподівання НВВ Х – це число, яке обчисл за формулою

f(x)-диференц. Ф-ія розп.

У практ д-ті під М(Х) розуміють центр розподілу ВВ і М(Х) приблизно дорівнює середньо арифметичному значенню ВВ.

Властивості М(Х):

1)М(С)=С, С=const

2)М(С*Y)=C*M(X), де С-сталий множник

3)М(Х+У)=М(Х)+М(У)

4)М(Ч*У)=М(Ч)*М(У)

Властивість 3 і 4 виконується тільки тоді, якщо х та у взаємно незамінні.

25. Дисперсія та середньоквадратичне відхилення: означення, властивості.

Дисперсією ВВ Х наз М(Х) квадрата відхилення цієї величини від її Н(Х)

Х-М(Х)-відхилення ВВ від М(Х)

Д(Х)=М

Для ДВВ Д(Х) обчислюється за формулою:

Для НВВ:

М(Х) показує центр розподілу ВВ, а Д(Х) показує розсіювання значень ВВ навколо М(Х)

Основні властивості Д(Х):

1)Д(С)=0,С=const

2)Д(С*Х)= *Д(Х)

3)Д(Х) 0

4)Д(Х У)=Д(Х)+Д(У)

Так як М(Х) вимірюється в лінійних одиницях(м,грн…), а Д(Х) вимірюється в кв.од.( , то для їх порівняння потрібно ввести наступну числову характеристику – це середнє квадратичне відхилення ( .