П. 1.1.2 Класс монотонных функций.

Здесь мы будем предполагать, что функция f не убывает на всей действительной оси (случай невозрастания функции рассматривается аналогично). Значит 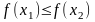для любых x₁ < x₂.

Для рациональных x доказано f(x) = x·f(1). Возьмём произвольное иррациональное x. Известно, что любое иррациональное число можно сколь угодно точно приблизить рациональными числами, поэтому для любого натурально q существует целое p такое, что

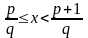(1.6)

и при достаточно больших q число x расположено между двумя очень близкими рациональными числами, разность между которыми равна 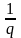. Используя монотонность функции f, находим

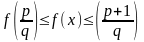
откуда (воспользовавшись соотношением для рациональных значений функции f)

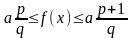, a = f(1). (1.7)

Так как из (1.3) f(0) = 0, то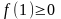 , ведь функция f не убывает, значит, .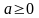

Если a = 0, то из неравенств 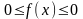имеем .

Если a = 0, то из (1.7)

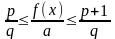. (1.8)

Сравнивая эти неравенства с (1.6), получим

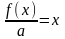
Покажем это. Предположим, что это неверно, например,

для выбранного иррационального x. Подберём q настолько большим, чтобы дробь 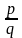попала между 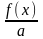и x

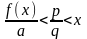
что противоречиво с (1.8). Полученное противоречие показывает, что

для любого заданного иррационального x, поэтому f(x) = ax для всех x.

п. 1.1.3 Класс ограниченных функций.

Пусть теперь функция f(x) ограничена с одной стороны (т. е. ограничена либо сверху, либо снизу) на каком-либо интервале (a, b). Нам нужно доказать, что линейными однородными функциями исчерпываются все решения (4) в данном классе. Мы исследуем решение уравнения (4), предполагая f ограниченной сверху (случай, когда f ограничена снизу, сводится к рассматриваемому случаю заменой f на -f).

Будем считать, что функция f ограничена сверху константой M, т. е. 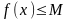для всех 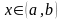. Рассмотрим вспомогательную функцию

g(x) = f(x) - x·f(1).

По доказанному выше g(x) = 0 при любом рациональном x. Кроме того, функция g(x) также является аддитивной. Действительно,

g(x + y) = f(x + y) - (x + y)·f(1) = f(x) + f(y) - xf(1) - yf(1) = g(x) + g(y).

Подставим y = r (r - рациональное) в равенство

g(x+y) = g(x)+g(y),

получим, учитывая g(r) = 0,

g(x+r) = g(x)+g(r) = g(x).

Значит, любое рациональное число r является периодом функции g(x).

Покажем теперь, что g(x) ограничена на интервале (a, b). Имеем

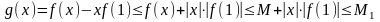
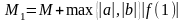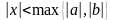где , поскольку при .

Отсюда тогда следует, что g(x) ограничена сверху на всей вещественной оси. В самом деле, для любого действительного x существует рациональное число r такое, что r (a-x, b-x), т. е. a < x+r < b. Поэтому

g(x) = g(x+r) < M1,

так как x + r (a, b), а на интервале (a, b) функция g ограничена числом M₁.

Сейчас уже можно утверждать, что g(x) = 0 для любого действительного x. Допустим это не так, т. е. для некоторого x₀

g(x₀) = A, A 0.

Поскольку для функции g(x), как для любой аддитивной функции, верно соотношение (1.1), то

g(nx₀) = ng(x₀) = nA

для любого целого n. Очевидно, что можно подобрать такое n (может быть, достаточно большое по абсолютной величине), что

nA > M₁, т.е. g(nx₀) > M₁.

Но функция g ограничена сверху константой M₁. Получаем противоречие. Значит, g(x) 0, откуда f(x) = x·f(1), что и требовалось.