§1. Уравнения Коши п. 1.1. Функциональное уравнение линейной однородной функции

Одним из наиболее исследованных в математике является функциональное уравнение Коши

f(x+y) = f(x) +f(y), D (f) =R (4)

Нетрудно заметить, что линейные однородные функции вида

f(x) = ax (a = const)

удовлетворяют этому уравнению:

f(x+y ) = a(x+y) = ax + ay = f(x) + f(y)

Вопрос состоит в том, будут ли эти функции единственными.

Прежде всего, выведем несколько общих фактов, не накладывая никаких ограничений на функцию f (т. е. без всяких предположений о непрерывности, ограниченности и т. п.).

Положим в уравнении y = x, получим:

f(2x) = 2f(x).

Далее, последовательно полагая y = 2x, y = 3x, y = 4x и т. д., имеем:

f(3x) = f(x+2x) = f(x)+f(2x) = f(x)+2f(x) = 3f(x);

f(4x) = f(x)+f(3x) = 4f(x);

f(5x) = f(x)+f(4x) = 5f(x),

и вообще, для любого натурального n

f(nx) = n·f(x) (1.1)

(это легко проверяется по индукции). Заменив здесь x на , мы получим

,

а затем, если подставить mx (m - натуральное) вместо x и использовать предыдущее равенство, придём к соотношению

, (1.2)

Положим теперь в основном уравнении (4) x = y = 0; получим

f(0) = 2f(0), так что f(0) = 0. (1.3)

Если же взять y = -x, то:

0 = f(x - x) = f(x) + f(-x)

f(-x) = -f(x),

так что функция f(x) является нечётной. А тогда из (1.1) легко вывести:

(1.4)

Полученные соотношения (1.2) – (1.4) могут быть объединены в равенстве

f(rx) = r·f(x),

справедливом для любого вещественного значения x, каково бы ни было рациональное число r.

Если взять здесь x = 1, то получим

f(r) = r·f(1) (1.5)

или, если обозначить f(1) через a, f(r) = ar.

Таким образом, мы, собственно говоря, установили уже вид функции f, но пока лишь для рациональных значений аргумента. При этом мы использовали только тот факт, что функция удовлетворяет основному уравнению Коши (4). Далее в решении мы будем уже опираться на конкретный класс функций, в котором ищется решение. Рассмотрим некоторые наиболее общие классы функций.

П. 1.1.1 Класс непрерывных функций

Для рациональных x мы установили, что f(x) = ax. Осталось показать, что это соотношение справедливо и для иррациональных x. Пусть x будет любое иррациональное число. Тогда существует последовательность рациональных чисел

,

сходящаяся к этому числу x (это известный факт; можно, например, взять отрезки соответствующей бесконечной десятичной дроби). По доказанному

f(r_n) = ar_n (n = 1,2,3, . . .).

Перейдём здесь к пределу при

Справа мы получим ax, слева же, именно ввиду предположенной непрерывности функции f, получится

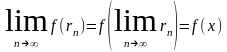
так что, окончательно,

f(x) = ax.

Таким образом, действительно, все непрерывные аддитивные функции являются линейными однородными. Последняя формула даёт самое общее решение функционального уравнения (4).